![]()
A partir do conceito de área, foi possível colocar e resolver o seguinte problema:
Se f é
uma função contínua em [a,b] e tal que 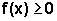 ,
para todo
,
para todo 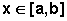 ,
então a área da região compreendida entre o eixo
x e o gráfico de f, para x variando em [a,b], é dada por:
,
então a área da região compreendida entre o eixo
x e o gráfico de f, para x variando em [a,b], é dada por:
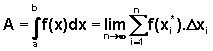 .
.
Entretanto, a definição de integral definida de uma função contínua num intervalo pode ser naturalmente estendida, sem a condição a respeito do sinal da função no intervalo dado. Assim,
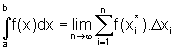 ,
desde que tal limite exista.
,
desde que tal limite exista.
Voltamos a frisar
que esse resultado somente representa a área da região
compreendida entre o eixo x e o gráfico de f, em
determinado intervalo, quando 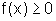 nesse intervalo.
nesse intervalo.
Se ![]() no intervalo [a,b] então
no intervalo [a,b] então 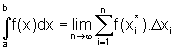 é
o valor do negativo da área da região compreendida entre
o eixo x e o gráfico de f, e as retas
é
o valor do negativo da área da região compreendida entre
o eixo x e o gráfico de f, e as retas ![]() e
e ![]() .
.
A integral definida verifica algumas propriedades:
![]() Se
f e g são funções integráveis
no intervalo [a,b], então a função f+g é
integrável em [a,b] e
Se
f e g são funções integráveis
no intervalo [a,b], então a função f+g é
integrável em [a,b] e 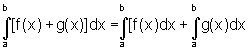 .
.
![]() Se k é uma constante e f é uma função
integrável no intervalo [a,b], então a função
k.f é integrável em [a,b] e
Se k é uma constante e f é uma função
integrável no intervalo [a,b], então a função
k.f é integrável em [a,b] e 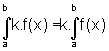 .
.
![]() Se
f é uma função integrável no intervalo
[a,b] e
Se
f é uma função integrável no intervalo
[a,b] e 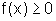 em [a,b] então
em [a,b] então 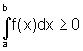 .
.
 Se
f é uma função integrável no intervalo
[a,b] e c é um ponto qualquer do intervalo [a,b], então
Se
f é uma função integrável no intervalo
[a,b] e c é um ponto qualquer do intervalo [a,b], então
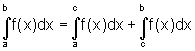 .
.
