![]()
Sabemos calcular a área de algumas figuras planas como, por exemplo, retângulos, triângulos, círculos e assim por diante. Dependendo da figura, esse problema está resolvido.
Imaginemos porém que o problema é o do cálculo da área do tampo de uma mesa que tem o seguinte formato:

Ou então, suponhamos que queremos revestir uma prancha de surf
e, portanto, queremos calcular a área da parte superior para
conhecer a quantidade de material a ser usado no revestimento.

Regiões desse tipo nos levam a perceber que as ferramentas de que dispomos para o cálculo de áreas não são suficientes.
Em primeiro lugar, vamos examinar figuras planas simples que são obtidas a partir do gráfico de alguma função conhecida.
![]() A área de um triângulo, como o da figura abaixo, que pode
ser obtido a partir do gráfico de
A área de um triângulo, como o da figura abaixo, que pode
ser obtido a partir do gráfico de 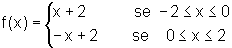
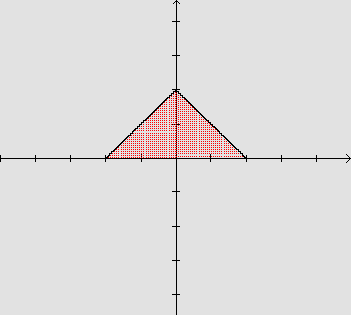
![]() A área de um triângulo, como o da figura abaixo, que pode
ser obtido a partir do gráfico de
A área de um triângulo, como o da figura abaixo, que pode
ser obtido a partir do gráfico de 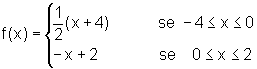
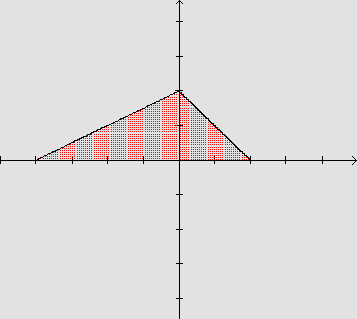
![]() A área da região compreendida entre o eixo x e o gráfico
da função:
A área da região compreendida entre o eixo x e o gráfico
da função:
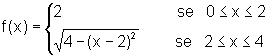
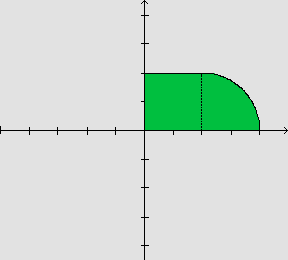
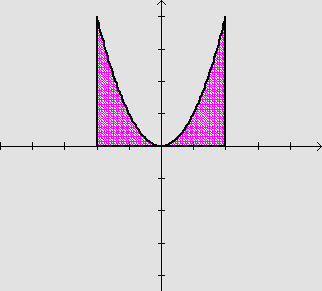
![]() A área da região que se encontra entre a parábola
y=x2 e o eixo x, para x variando no intervalo [-2,2].
A área da região que se encontra entre a parábola
y=x2 e o eixo x, para x variando no intervalo [-2,2].