Volumes de Sólidos
1. Volume de um sólido quando é conhecida a área
de qualquer secção transversal.
![]() Usando o Cálculo Integral, mostre que o volume de uma pirâmide
reta de base quadrada - sendo b a medida da aresta da base e
h a altura da pirâmide - é
Usando o Cálculo Integral, mostre que o volume de uma pirâmide
reta de base quadrada - sendo b a medida da aresta da base e
h a altura da pirâmide - é 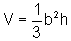 .
.
![]() Usando o Cálculo Integral, mostre que o volume de um cilindro
reto, de altura h e cuja base é um círculo de raio
r, é
Usando o Cálculo Integral, mostre que o volume de um cilindro
reto, de altura h e cuja base é um círculo de raio
r, é 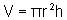 .
.
![]() Usando
o Cálculo Integral, mostre que o volume de um cone reto, de altura
h e cuja base é um círculo de raio r, é
Usando
o Cálculo Integral, mostre que o volume de um cone reto, de altura
h e cuja base é um círculo de raio r, é
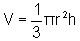 .
.
Nesses problemas observamos que temos um sólido compreendido
entre dois planos paralelos e que é conhecida a área da
secção transversal obtida por um plano qualquer paralelo
aos planos inicialmente dados, então o volume do sólido
é dado por
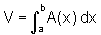 ou
ou 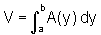
conforme a secção transversal seja perpendicular ao eixo x ou y, respectivamente.
Essa é uma primeira maneira de encontrarmos o volume de um sólido, quando a área de qualquer secção transversal é conhecida.
2. Volume de um sólido de revolução, obtido
pela rotação em torno ao eixo x - ou y - de um conjunto
A.
Seja f uma função
contínua num intervalo 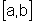 ,
sendo
,
sendo 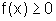 para todo x, tal que
para todo x, tal que 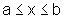 .
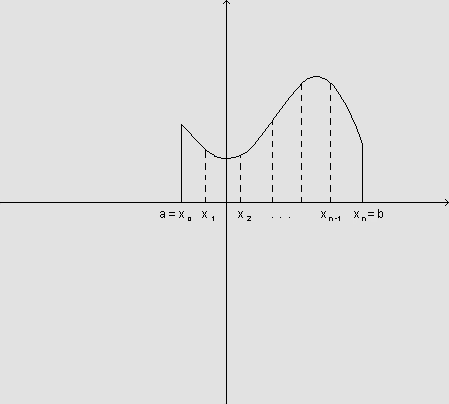
Consideremos o conjunto A, delimitado pelo eixo x, o gráfico
de f e as retas x=a e x=b:
.
Consideremos o conjunto A, delimitado pelo eixo x, o gráfico
de f e as retas x=a e x=b:
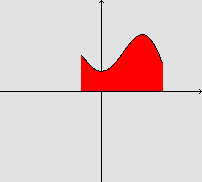
Seja B o sólido obtido através da rotação do conjunto A em torno do eixo x.
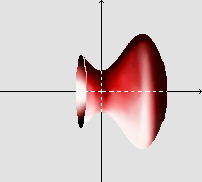
Considerando uma partição
P do intervalo 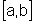 :
:
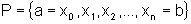 ,
tal que
,
tal que 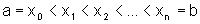 ,
seja:
,
seja:
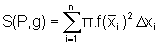 onde
onde 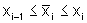 para todo i,
para todo i, 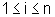 ,
,
que é uma
soma
de Riemann para a função 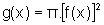 ,
relativa à partição P do intervalo
,
relativa à partição P do intervalo 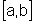 .
.
Definimos o volume do sólido B como sendo:
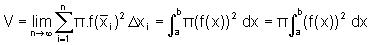 .
.
É preciso
observar que cada secção transversal do sólido
B, obtida a partir de x, 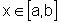 ,
é um círculo centrado no ponto
,
é um círculo centrado no ponto 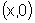 e
raio f(x) e, portanto, cuja área é
e
raio f(x) e, portanto, cuja área é 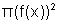 .
.
![]() Seja
Seja 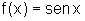 ,
,
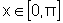 .
Calcule o volume do sólido gerado pela rotação
do gráfico de f, ou seja pela rotação da
região delimitada pelo eixo x, o gráfico de f
e as retas x = 0 e
.
Calcule o volume do sólido gerado pela rotação
do gráfico de f, ou seja pela rotação da
região delimitada pelo eixo x, o gráfico de f
e as retas x = 0 e ![]() .
.
![]() Considere a região do plano delimitada pelo eixo x, o gráfico
de
Considere a região do plano delimitada pelo eixo x, o gráfico
de 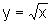 ,
para
,
para 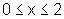 ,
sendo girada primeiro ao redor do eixo x e depois ao redor do eixo y.
Calcule o volume dos dois sólidos gerados.
,
sendo girada primeiro ao redor do eixo x e depois ao redor do eixo y.
Calcule o volume dos dois sólidos gerados.
3. Volume de um sólido pelo método dos invólucros
cilíndricos.
Podemos imaginar o sólido como sendo constituído por cascas cilíndricas.
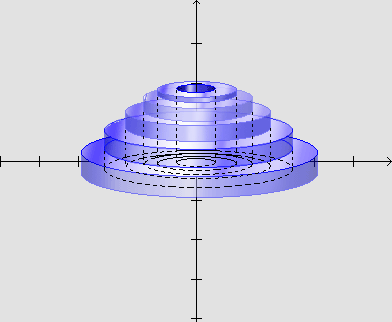
O volume de cada uma das cascas é dado por:
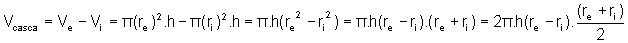
(o índice “e” refere-se a externo e o índice “i” refere-se a interno)
ou ainda, colocando 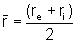 e
e 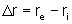 ,
,
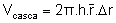
Seja f uma função
contínua num intervalo 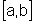 ,
com
,
com 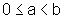 .
Consideremos o conjunto A, delimitado pelo eixo x, o gráfico
de f e as retas x=a e x=b. Suponhamos que a região gira
ao redor do eixo y, gerando um sólido D, cujo volume queremos
calcular.
.
Consideremos o conjunto A, delimitado pelo eixo x, o gráfico
de f e as retas x=a e x=b. Suponhamos que a região gira
ao redor do eixo y, gerando um sólido D, cujo volume queremos
calcular.

Observemos as cascas cilíndricas compondo o sólido gerado:
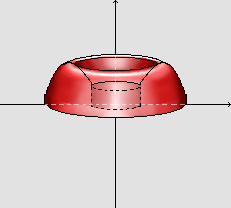
Por esse processo, o volume do sólido composto das cascas cilíndricas
é dado por:
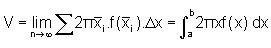
onde 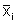 indica o raio de cada invólucro e
indica o raio de cada invólucro e 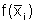 indica sua altura.
indica sua altura.
![]() Através do método dos invólucros cilíndricos
encontre o volume do sólido gerado pela rotação
da região do plano delimitada pelo eixo x, o gráfico
de
Através do método dos invólucros cilíndricos
encontre o volume do sólido gerado pela rotação
da região do plano delimitada pelo eixo x, o gráfico
de 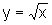 ,
para
,
para 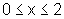 ,
ao redor do eixo y.
,
ao redor do eixo y.
![]() Encontre o volume do sólido obtido pela rotação
da região compreendida entre os gráficos de
Encontre o volume do sólido obtido pela rotação
da região compreendida entre os gráficos de 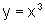 e
e 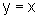 ,
para
,
para 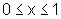 ,
ao redor do eixo y.
,
ao redor do eixo y.
