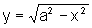Considere a região delimitada por , o eixo x e as retas x=-a e x=a , sendo girada ao redor do eixo x. O sólido originado é uma esfera de raio a. Mostre que seu volume é .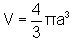

Calcule o volume de um sólido de revolução obtido pela rotação ao redor do eixo x da região compreendida pelo gráfico d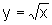e e 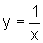, no intervalo 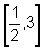. Calcule também o volume do sólido obtido ao girar a mesma região ao redor do eixo y.

Calcule o volume do sólido obtido pela rotação, em torno ao eixo x, do conjunto de todos os pontos (x,y) tais que 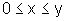e .

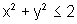Calcule o volume do sólido obtido pela rotação, em torno ao eixo x, do conjunto: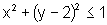 .