![]()
Consideremos uma semi-reta
OA, tal que o comprimento do segmento OA seja unitário.
Escolhemos também um referencial cartesiano tal que o semi-eixo
x positivo coincida com a semi-reta OA e o semi-eixo y positivo seja obtido
girando a semi-reta OA no sentido anti-horário, de 90o
ou 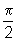 radianos.
Dessa maneira, temos o modelo geométrico que é a circunferência
trigonométrica.
radianos.
Dessa maneira, temos o modelo geométrico que é a circunferência
trigonométrica.
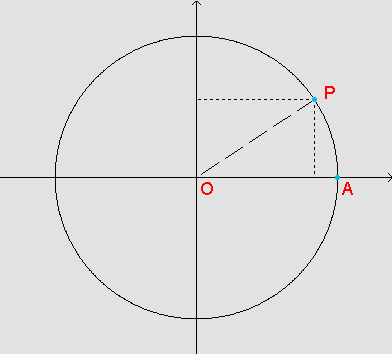
Dado um número real x, associamos a ele o ponto P=P(x) no
círculo unitário, de tal modo que o comprimento do arco
AP é x unidades de medida de comprimento, ou seja, a medida
do arco AP é x radianos. Também
podemos dizer que o arco AP e, portanto, o ângulo central 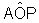 tem
tem 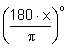 .
.
Definimos as funções seno, cosseno e tangente do número real x da seguinte maneira:
cos x: é
a abscissa de P
sen x: é a ordenada de P
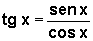 , se
, se 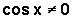
Desse modo, dado um número x real, fica determinado, na circunferência trigonométrica, o ponto:
P=P(x)=(cos x, sen x).
Como conseqüência das definições de sen x,
cos x e tg x, temos que:
· P(0)
= A = (1,0) e, portanto, cos 0 =
1, sen 0 = 0, tg 0 =
0.
· P = (0,1) e, portanto, cos
= (0,1) e, portanto, cos 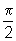 = 0, sen
= 0, sen 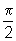 =1, enquanto tg
=1, enquanto tg 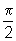 não existe, pois cos
não existe, pois cos 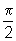 = 0.
= 0.
Propriedades:
i) Dados P(x) = (cos x, sen x) e P(-x) = (cos(-x), sen(-x)), pode-se provar que
cos(-x)=cos x e sen(-x)=-sen(x). E a tg(x)?
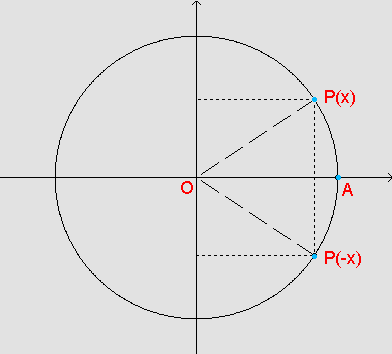
Dessa maneira, concluímos que P(-x) é o ponto simétrico de P(x) em relação ao eixo horizontal.
Também notamos que cos é uma função par, e que sen é uma função ímpar
ii) Dados os pontos:
P(x)=(cos x, sen x)
e 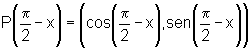 ,
,
pode-se provar que 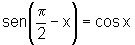 e que
e que 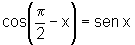 .
E a
.
E a 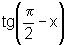 ?
?
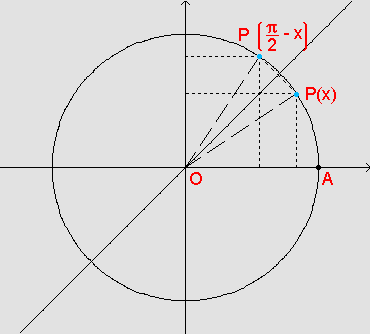
Dessa maneira, temos
que 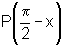 é
o ponto
simétrico de P(x) em relação à reta y
= x, que é a bissetriz do primeiro e terceiro quadrantes.
é
o ponto
simétrico de P(x) em relação à reta y
= x, que é a bissetriz do primeiro e terceiro quadrantes.
A
partir das propriedades acima, é possível mostrar que:
iii) sen 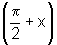 =cos
x e cos
=cos
x e cos 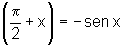 ;
;
iv) 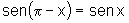 e
e 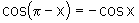 ;
;
v) 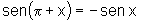 e
e 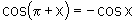 ;
;
vi) 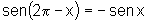 e
e 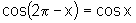 ;
;
vii) 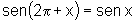 e
e 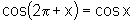 .
.
Através dessas propriedades, dado um número real x qualquer, determinamos um arco e, portanto, um ângulo central correspondente, e sabemos determinar o seno e o cosseno desse número real, não importando em qual quadrante se encontre o ponto P(x). Essas relações são conhecidas como fórmulas de redução ao primeiro quadrante, pois nos permitem encontrar o seno e o cosseno de um número real qualquer, em termos daquele outro número real que determina um arco no primeiro quadrante.
Finalmente, utilizando a circunferência trigonométrica, é possível mostrar que, para todos a e b reais, valem as relações:
cos(a+b) = cos a.cos b-sen a.sen b
sen(a+b)
= sen a.cos b+sen b.cos a
que permitem calcular o seno e o cosseno da soma de dois arcos em termos
do seno e cosseno desses arcos separadamente considerados.
Uma
questão que se coloca é a seguinte: essas funções
têm qual relação com aquelas de mesmo nome - que,
para fazer uma distinção, nomeamos com inicial maiúscula
- que foram definidas no triângulo retângulo?
