Verifique que, para todo número real x, temos 
.
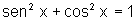Quais são os valores máximos e mínimos para sen x
e para cos x? Qual a imagem de cada uma das duas funções?
Verifique que, para todo número inteiro k e para todo número
real x, temos: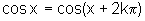 
.
Isso significa que a função cos é periódica,
de período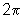 
.
Vale o mesmo para a função sen? Esboce o gráfico
de y=sen x e de y=cos x. Para isso, considere x variando e examine o que
acontece com seu seno e seu cosseno.
Para quais valores de x é possível definir tg x?
Qual a imagem da função tg? Esboce o gráfico
de y=tg x.
Utilizando
a circunferência trigonométrica, calcule sen, cos e tg dos
arcos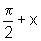 
, 
, 
, 
,
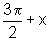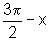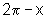em termos de sen x, cos x e tg x, sendo x um número entre 0 e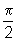 
.
Mostre que cos(a-b)=cos a.cos b+sen a.sen b, para quaisquer a
e b reais.
.
Some
as fórmulas para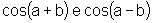 
e deduza uma fórmula para o produto 
.
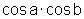Por analogia, deduza uma fórmula para 
.
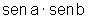Nas fórmulas do produto faça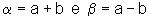 
e mostre que
 |
 |
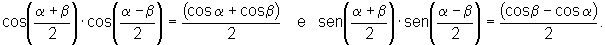
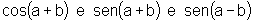