A função do segundo
grau mais simples é a função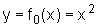 
. Todo ponto de seu gráfico é da
forma 
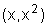, ou seja, a ordenada de cada ponto
é o quadrado da abscissa.
A curva obtida denomina-se
parábola:
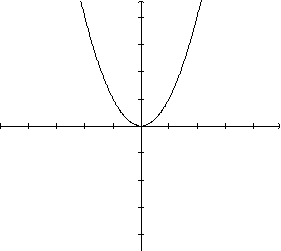
O objetivo aqui é o de descobrir como é o gráfico da função do segundo grau y=ax2+bx+c, onde
,
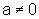quando comparado ao gráfico de y=x2, observando as transformações
realizadas, dependendo dos parâmetros a, b e c.
Para adquirir essa compreensão, começamos com situações mais simples,
tendo sempre como referência o gráfico de y=x2.
Em
primeiro lugar, consideremos uma função do segundo grau da forma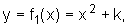 
onde k é uma constante real.
Comparando seu gráfico ao da função y=x2, temos a questão:
qual a ação da constante k no gráfico dessa nova função quando
comparado ao gráfico da função inicial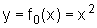 
?
Ainda podemos pensar numa função do segundo grau que seja dada pela
expressão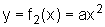 
onde a é uma constante real,
com 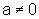. Observemos que, se a=0, a função
obtida não será do segundo grau, pois será a função constante nula.
Novamente, a questão é investigar a ação do coeficiente a quando
comparamos o gráfico de f2 ao de f0.
Construa o gráfico de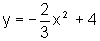 
,
a partir do gráfico de y=x2, esboçando os gráficos intermediários,
todos num mesmo par de eixos, a fim de visualizar as transformações
realizadas. Em seguida, num outro par de eixos, construa o gráfico de
y=3x-2, observando também as transformações realizadas a partir de y=x.
Finalmente, “passando a limpo” os gráficos das duas funções, resolva
a inequação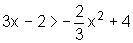 
, verificando
no gráfico, o significado das operações algébricas a serem realizadas.
Uma questão que também se coloca é a consideração de funções do segundo
grau do tipo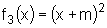 
onde m é um número real
não nulo. Qual é a ação de m no gráfico da função f3 quando
comparado ao gráfico de f0, isto é à parábola inicial?
Se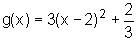 
desenhe seu gráfico, fazendo os
gráficos intermediários, todos num mesmo par de eixos.
Finalmente, podemos considerar funções do segundo grau do tipo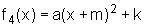 
examinando as transformações do
gráfico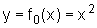 
quando fazemos y=(x+m)2,
em seguida, y=a(x+m)2 e, finalmente,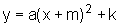
. Observe que o coeficiente a
não pode ser zero.
Por
quê?
y=a(x+m)2+k
Conclusão: Conhecido
o gráfico de y=x2, podemos desenhar y=(x+m)2,
para, em seguida, desenhar y=a.(x+m)2 e depois, y=a.(x+m)2+k.
Analisemos o que aconteceu:
- a seguir, no gráfico de y=a.(x+m)2 ocorreu mudança de inclinação pois em cada ponto a ordenada é igual àquela do ponto de mesma abscissa em
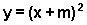multiplicada pelo coeficiente a;- finalmente, o gráfico de y=a.(x+m)2+k sofreu uma translação vertical de k unidades, pois, para cada abscissa, as ordenadas dos pontos do gráfico de y=a.(x+m)2+k ficaram acrescidas de k, quando comparadas às ordenadas dos pontos do gráfico de y=a.(x+m)2.
Assim, quando a função do segundo grau está dada nessa forma, temos claro o que está acontecendo pois as operações a serem realizadas no gráfico ficam explícitas. Entretanto, muitas vezes, nos defrontamos com uma função do segundo grau cuja expressão é da forma y=ax2+bx+c, com a não nulo. A questão que emerge é: como vamos entender seu gráfico em termos de transformações no plano quando fazemos a comparação com o gráfico de y=x2, pois os movimentos a serem realizados não estão claros.
Desenhe o gráfico da função dada por y=3x2-5x+4, explicitando
as transformações realizadas a partir do gráfico de y=x2.
Se
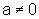, y=ax2+bx+c
pode ser escrita na forma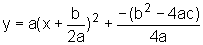 
.
Podemos verificar como é o gráfico dessa função, comparando-a com a
função mais simples y=x2 e realizando translações ou mudança
de inclinação.
Conclusão: A função do segundo grau f(x)=ax2+bx+c,
com a não nulo, tem como domínio
o conjunto R, pois a variável independente pode assumir qualquer valor.
A imagem
é o conjunto
 |
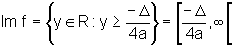ou
|
 |
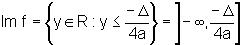conforme a>0
ou a<0, respectivamente. De fato, 
é a ordenada do vértice da parábola.
O estudo dos gráficos das funções envolvidas auxilia na resolução de equações ou inequações, pois as operações algébricas a serem realizadas adquirem um significado que é visível nos gráficos das funções esboçados no mesmo referencial cartesiano.
 |
 |