Definição - Hipérbole
Sejam dados dois números reais positivos a e c tais que c>a.
Consideremos dois pontos F1
e F2 tais que d(F1,F2)=2c e seja um plano
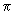passando
por F1 e F2, com um sistema de eixos cartesianos
Oxy, tal que F1 e F2 estejam no eixo x e a origem
do sistema seja o ponto médio do segmento 
.
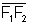Dessa forma, F1=(c,0) e F2=(-c,0).
Vamos examinar o lugar geométrico
dos pontos P=(x,y) do plano
tais que:
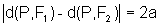< 2c
Nas condições dadas, é possível
deduzir a equação
mais simples que descreve o lugar geométrico, obtendo: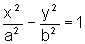 
,
onde b2=c2-a2.
Assim, podemos escrever a definição do lugar geométrico determinado pela equação que foi deduzida.
Definição: Nas condições
descritas acima, o lugar geométrico dos pontos P tais que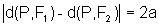 
é uma curva denominada hipérbole de focos F1 e F2,
com distância focal 2c e distância entre os vértices 2a.
O gráfico
da equação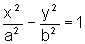
é o seguinte:
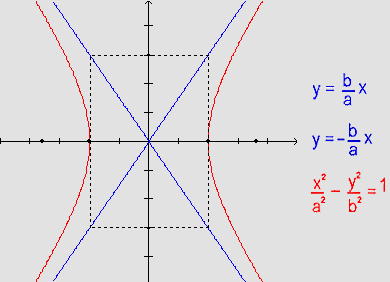
As retas r: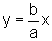 
e s: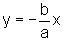
são chamadas
assíntotas
à hipérbole.
Observações:
1. Dada a equação ,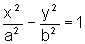
a distância focal 2c é determinada através da relação c2=a2+b2.
2. Se o eixo y passar pelos focos e o eixo x pelo ponto médio de ,
isto é, F1=(0,c) e F2=(0,-c), então a equação da
hipérbole será do tipo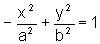 
e a curva terá o seguinte aspecto:
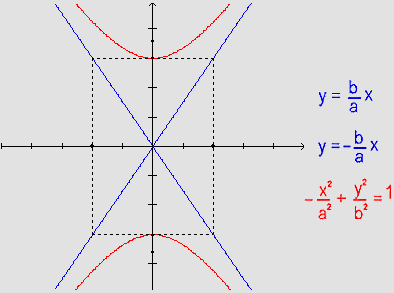
Uma hipérbole particular é
o gráfico de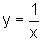 
.
Seus focos são os pontos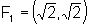 
e 
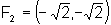, ou
seja, qualquer ponto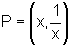 
que pertence à curva, satisfaz à definição 
.
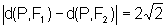Uma vez que a variável independente x não pode ser zero, observamos que a curva não intercepta o eixo vertical.
Entretanto, conforme x assume valores
positivos, próximos de zero, a variável dependente y assume valores
muito grandes, positivos. Escrevemos isso sucintamente,
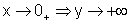
Por outro lado, conforme x assume valores negativos, próximos de zero, a variável dependente y assume valores muito grandes negativos, o que pode ser escrito:
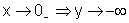
Outro fato visível no gráfico é que quando x cresce, sendo muito grande e positivo, o valor de y é muito pequeno, ainda positivo, isto é,
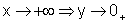
Finalmente, quando x é muito grande, mas negativo, o valor de y é muito pequeno, negativo, ou seja
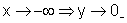
O eixo vertical - que é a reta de equação x=0 - e o eixo horizontal - que é a reta de equação y=0 - são denominadas assíntotas ao gráfico da função. São retas das quais o gráfico se aproxima indefinidamente, sem nunca encostar.
 |
 |