O conceito de módulo de um número real está associado à idéia de distância
de um ponto da reta à origem. Como existe uma correspondência
biunívoca entre os pontos da reta e os números reais, pensar na distância
de um ponto à origem ou pensar no módulo de um número é exatamente a mesma
coisa.
Assim,
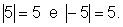
pois o número 5 está a uma distância de 5 unidades
da origem, e -5 também está a 5 unidades da origem.
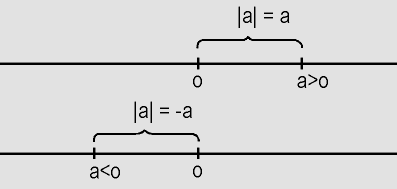
De modo geral podemos dizer que:
- se a>0,
,
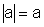- se a<0,
,
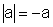- se a=0,
.
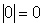Definimos então uma função que, a cada número real x associa o módulo de x, ou seja, a distância de x à origem. Temos assim:
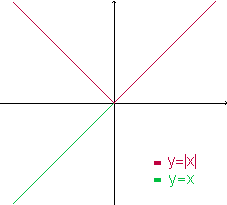
O gráfico dessa função tem o seguinte aspecto:
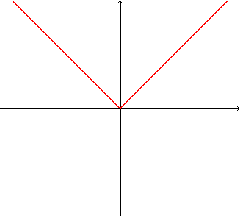
pois, para os valores positivos
ou zero da variável independente x, o valor da variável dependente y é
o mesmo que x, pois y=x; para valores negativos de x o valor de y é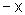 
,
pois y=-x. Dessa forma, o gráfico é constituído
de duas semi-retas de mesma origem.
Outra maneira interessante de olhar para o gráfico de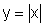 
é considerar que ele coincide com a reta y=x para valores de x positivos
ou zero, enquanto que para valores negativos de x, tomamos a semi-reta
"rebatida", pois, nesse caso,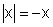 
.
Esta semi-reta "rebatida", evidentemente, é simétrica
da original em relação ao eixo horizontal.
Essa última consideração nos permite rapidamente entender como será o
gráfico de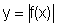 
para
uma dada função f conhecida. De fato,
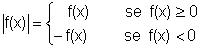
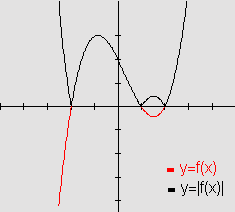
e, portanto seu gráfico
i) coincide com o gráfico de f
para todos os valores da variável independente x nos quais a variável
dependente é positiva ou zero;
ii) é o "rebatido" ou o simétrico do gráfico de f para todos os valores
da variável independente x nos quais a variável dependente é negativa.
Dada uma função f, podemos pensar na função g(x)=f(
).
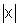De fato, pela definição da função valor absoluto de um número real, a
função g pode ser entendida como sendo
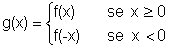
isto é, para x assumindo valores positivos ou zero, a função g coincide com a função f; para x assumindo valores negativos, a função g é igual à função f calculada no oposto de x.
Assim:
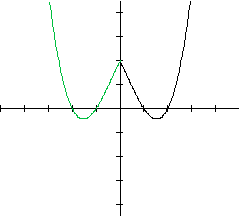
ou seja, o gráfico de g apresenta simetria em relação ao eixo vertical.
 |
 |