Examinemos algumas funções, seus respectivos gráficos e imagens:
![]() Dada a função
Dada a função 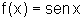 .
O que podemos dizer sobre a imagem da função?
.
O que podemos dizer sobre a imagem da função?
![]() Dada a função
Dada a função 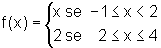 .
O que podemos dizer sobre a imagem de f?
.
O que podemos dizer sobre a imagem de f?
![]() Analise a imagem da função
Analise a imagem da função 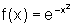 através de seu gráfico.
através de seu gráfico.
Definição:
Uma função f é dita limitada, em seu domínio,
quando sua imagem está contida num intervalo, ou seja, 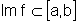 ,
onde a,b
,
onde a,b 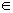 R. Podemos também utilizar a seguinte notação:
R. Podemos também utilizar a seguinte notação:
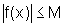 , sendo
, sendo 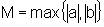 .
.
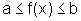 para todo
para todo 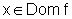 ,
então podemos examinar qual dos dois números,
,
então podemos examinar qual dos dois números, 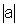 ou
ou 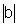 é o maior e chamamos
é o maior e chamamos 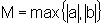 .
.Assim, podemos dizer que
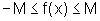 ou que
ou que 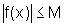 .
.No caso de uma função
contínua em R, a análise dos limites
quando 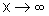 ou
ou
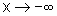 , nos fornece
a informação necessária para decidir sobre a existência
ou não de um limitante para a função.
, nos fornece
a informação necessária para decidir sobre a existência
ou não de um limitante para a função.
![]() Seja
f uma função limitada. Uma pergunta natural que surge é:
a função
Seja
f uma função limitada. Uma pergunta natural que surge é:
a função 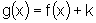 ,
,
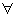 k
k 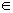 IR, cujo gráfico é o resultado de uma translação
vertical de k unidades no gráfico de f, também é
limitada?
IR, cujo gráfico é o resultado de uma translação
vertical de k unidades no gráfico de f, também é
limitada?
![]() Seja f uma função limitada. A função
Seja f uma função limitada. A função
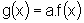 ,
, 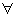 a
a
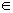 IR, também
é limitada? Em outras palavras, se provocamos uma mudança
de inclinação no gráfico de f, ainda sim temos
o gráfico de uma função limitada?
IR, também
é limitada? Em outras palavras, se provocamos uma mudança
de inclinação no gráfico de f, ainda sim temos
o gráfico de uma função limitada?
![]() Seja f uma função limitada. A função
Seja f uma função limitada. A função
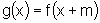 ,
, 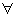 m
m
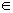 IR, cujo
gráfico é o resultado de uma translação horizontal
no gráfico de f, também é limitada?
IR, cujo
gráfico é o resultado de uma translação horizontal
no gráfico de f, também é limitada?
![]() Seja f uma função limitada. A função
Seja f uma função limitada. A função
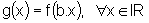 , também
é limitada?
, também
é limitada?
![]() Dada as funções limitadas f e g, uma pergunta
que surge é: a função soma f+g é uma
função limitada?
Dada as funções limitadas f e g, uma pergunta
que surge é: a função soma f+g é uma
função limitada?
![]() Dada as funções limitadas f e g, a função
produto f.g é uma função limitada?
Dada as funções limitadas f e g, a função
produto f.g é uma função limitada?

