Examinando gráficos de funções observamos que, em certo sentido, alguns deles apresentam características especiais. Isso é um tanto vago, entretanto, conhecer algumas dessas características, muitas vezes, pode auxiliar no estudo e compreensão do gráfico de uma função mais complicada.

- Simetria em relação ao eixo vertical

É, por exemplo o caso de:

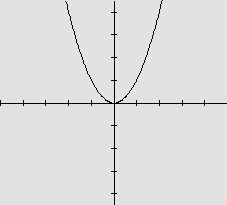O gráfico de f(x)=x2

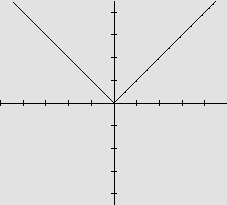O gráfico de f(x)=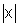

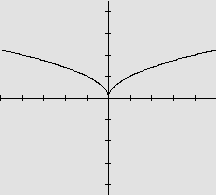O gráfico de f(x)=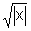

Uma função, cujo gráfico apresenta simetria em relação ao eixo vertical, é tal que, para todo ponto do gráfico (x,f(x)), o ponto (-x,f(-x)), com f(x)=f(-x), também está no gráfico.

Uma tal função é denominada função par. Formalmente, dizemos que:

Definição: Uma função f é denominada par quando f(x)=f(-x), para todo x do Dom f.

Analogamente, podemos observar um outro tipo de simetria que muitas vezes ocorre.

• Simetria em relação à origem.
  Por exemplo, temos:
  

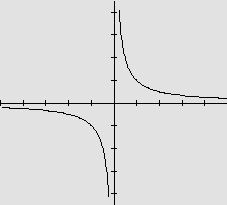O gráfico de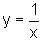

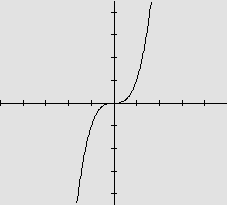O gráfico de y=x3

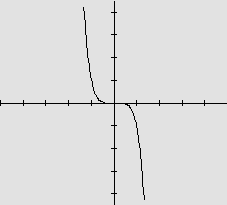O gráfico de y=-x5

Nos gráficos acima observamos a simetria em relação à origem, pois, para todo ponto da forma (x,f(x)), o ponto (-x,f(-x)), com f(x)= -f(-x), também está no gráfico. Uma função com essa característica é denominada função ímpar. Formalmente, temos:

Definição: Uma função f é denominada ímpar quando f(x)=-f(-x), para todo x do Dom f.

Saber que uma função é par ou ímpar simplifica o estudo do seu comportamento pois, para essas classes de funções, conhecendo o que acontece para x>0 pode-se, utilizando os argumentos de simetria, inferir o que acontece em todo domínio da função.

Entretanto, existem funções cujos gráficos não possuem essas características. É o caso, por exemplo, de
f(x)=ln x

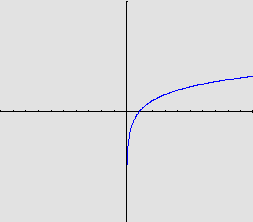
ou de

f(x)= e^x

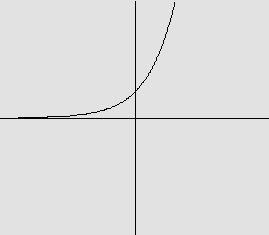
mas mesmo para essas funções há uma propriedade interessante que pode ser analisada no Exercício 3.