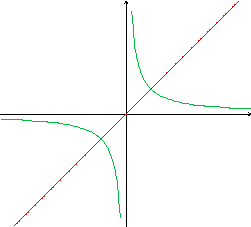
Observemos os gráficos de f(x)=x e g(x)= :

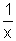Num programa gráfico, por exemplo no Winplot, podemos plotar o gráfico de 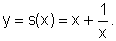Obtendo então:

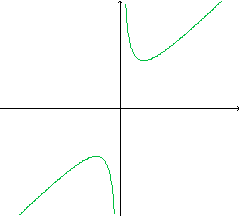
Qual o significado desse novo gráfico?

A primeira coisa que nos chama a atenção é a de que, para cada valor da variável independente x para o qual existem f(x) e g(x), o valor de s(x) é a soma dos valores das duas funções separadamente consideradas.

No caso, como g não está definida para x=0, isto é, não existe g(0), a função s também não existe para x=0. De fato, só existe a função s para aqueles valores nos quais as funções f e g estão definidas. Ou seja

.

Também poderíamos considerar, de modo análogo, a função d(x)=f(x)-g(x), que é a diferença entre as duas funções dadas inicialmente, e cujo domínio será

.

Em lugar de somar ou subtrair as duas funções para obter uma nova função, poderíamos, por exemplo, considerar o produto de f por g, obtendo a função, :

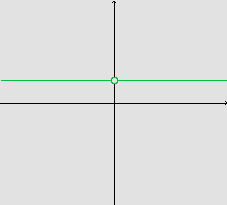
No caso, obtemos , ou seja, p é uma função constante; pois não existe g(0), logo p(0) também não existe. Assim temos que a nova função p está definida para aqueles valores em que as funções f e g estão definidas. Ou seja

.

A produção de novas funções pode ser assim generalizada, tomando um cuidado adicional quando fazemos o quociente de duas funções. De fato, considerando , temos uma função definida para x , que pode ser encarada como obtida a partir do quociente de duas funções, h(x)=x+1 e f(x)=x, ambas definidas para todo valor de x. Podemos dizer que

ou seja, o domínio da função quociente é a intersecção dos domínios das duas funções retirando o conjunto dos valores que anulam o denominador.