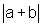
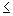
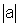 +
+
Vamos fazer a demonstração de duas maneiras:
i) Utilizando gráficos
de funções e, nesse caso, vamos mostrar que 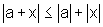 ,
para todos x e a reais.
,
para todos x e a reais.
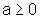 ,
então
,
então 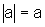 .
.
Sejam então,
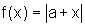 e
e 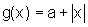 . Vamos mostrar
que o gráfico de f está abaixo ou coincide com o
gráfico de g e, portanto,
. Vamos mostrar
que o gráfico de f está abaixo ou coincide com o
gráfico de g e, portanto, 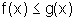 ,
para todo x real.
,
para todo x real.
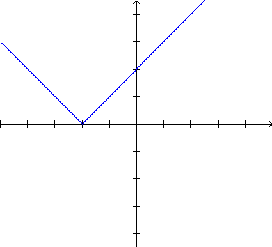 |
O
gráfico de 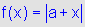 ,
com ,
com 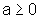 |
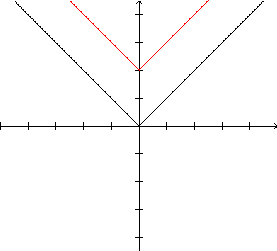 |
O
gráfico de
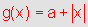 ,
com ,
com 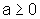 , ,e o gráfico de 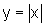 |
Comparando os gráficos de f e g, verificamos que
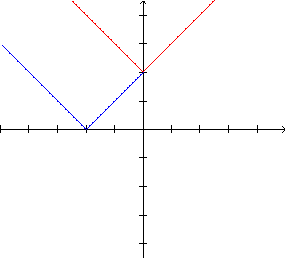 |
Para 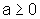 :
:o gráfico de 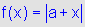 e o gráfico de 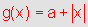 |
ou seja 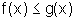 ,
para todo x real, o que demonstra a tese para o caso
,
para todo x real, o que demonstra a tese para o caso 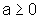 .
.
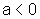 ,
então
,
então 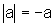 .
.
Sejam então,
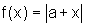 e
e 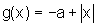 . Vamos
mostrar que o gráfico de f está abaixo ou coincide
com o gráfico de g e, portanto,
. Vamos
mostrar que o gráfico de f está abaixo ou coincide
com o gráfico de g e, portanto, 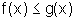 ,
para todo x real.
,
para todo x real.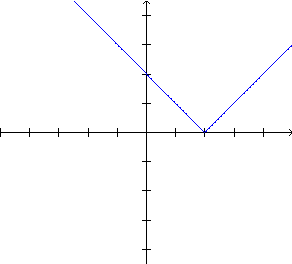 |
O gráfico
de 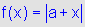 ,
com a<0 ,
com a<0 |
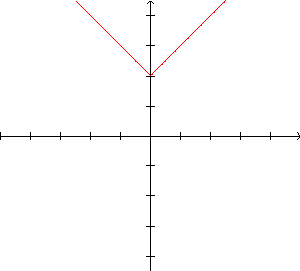 |
O gráfico
de 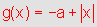 ,
com a<0 ,
com a<0 |
Comparando os gráficos
de f e g,
verificamos que
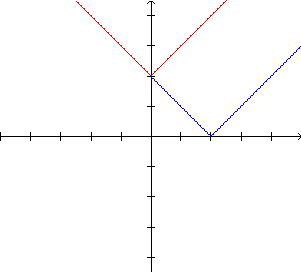 |
Para a<0: o gráfico de 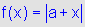
e o gráfico de 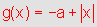 |
ou seja 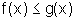 ,
para todo x real, o que demonstra a tese para o caso a<0.
,
para todo x real, o que demonstra a tese para o caso a<0.
Dessa forma, mostramos,
graficamente, que 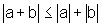 ,
para todos a e b reais.
,
para todos a e b reais.
ii) Algebricamente, vamos provar que 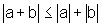 ,
para todos a e b reais.
,
para todos a e b reais.
Temos dois casos a considerar:
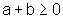 ,
então
,
então 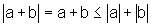 ,
pois todo número é sempre menor ou igual ao seu valor
absoluto. Assim, nesse primeiro caso, mostramos que
,
pois todo número é sempre menor ou igual ao seu valor
absoluto. Assim, nesse primeiro caso, mostramos que 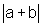
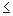
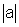 +
+ .
.
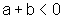 ,
então
,
então 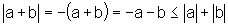 ,
pois o oposto de um número é sempre menor ou igual ao
valor absoluto desse número. Assim, também nesse caso,
mostramos que
,
pois o oposto de um número é sempre menor ou igual ao
valor absoluto desse número. Assim, também nesse caso,
mostramos que 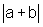
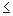
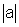 +
+ .
. |
