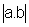 =
= 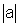 .
. 
Vamos fazer a demonstração de duas maneiras:
i) Utilizando gráficos
de funções e, nesse caso, vamos mostrar que 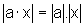 ,
para todos x e a reais.
,
para todos x e a reais.
- Se
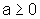 ,
então
,
então 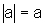 .
.
Sejam então,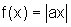 e
e 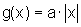 . Vamos
mostrar que os gráficos de f e g coincidem e, portanto,
f(x)=g(x), para todo x real.
. Vamos
mostrar que os gráficos de f e g coincidem e, portanto,
f(x)=g(x), para todo x real.
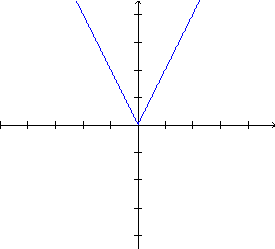 |
O
gráfico de 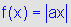 ,
com ,
com 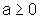 |
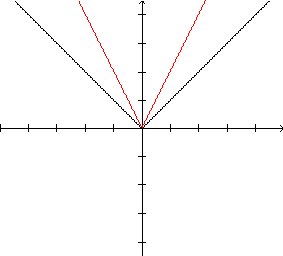 |
O
gráfico de 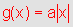 ,
com ,
com 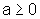 , ,e o gráfico de 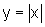 |
- Se
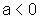 ,
então
,
então 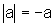 .
.
Sejam então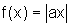 ,
e
,
e 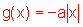 . Vamos
mostrar que os gráficos de f e g coincidem e, portanto,
f(x)=g(x), para todo x real.
. Vamos
mostrar que os gráficos de f e g coincidem e, portanto,
f(x)=g(x), para todo x real.
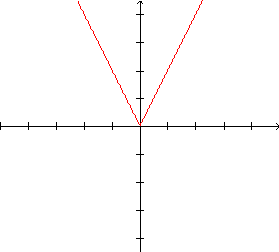 |
O
gráfico de 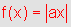 ,
com ,
com 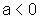 |
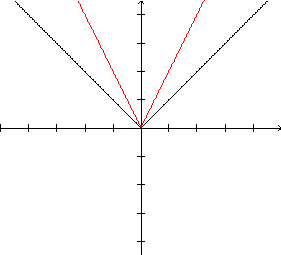 |
O gráfico
de 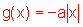 , com , com
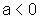 , ,e o gráfico de 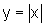 |
Assim, graficamente,
observamos que 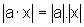 ,
para todos x e a reais.
,
para todos x e a reais.
ii) Algebricamente,
vamos provar que 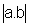 =
=
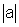 .
.  ,
para todos a e b reais.
,
para todos a e b reais.
Temos que: 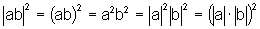
Como 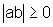 e
e 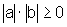 então,
extraindo a raiz quadrada de ambos os lados da igualdade, temos
então,
extraindo a raiz quadrada de ambos os lados da igualdade, temos 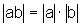 ,
como queríamos demonstrar.
,
como queríamos demonstrar.
 |
