Propriedade
Fundamental das áreas das regiões do tipo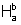 
:
Considerando
o gráfico da função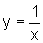 
,
para x variando no intervalo [a,b], obtemos uma região do plano
delimitada pelo eixo horizontal, o gráfico da referida função e as retas
verticais x=a e x=b.
As regiões desse tipo gozam da seguinte propriedade:
Consideremos
k>0 e 0<a<b: as faixas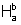
e 
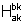têm a
mesma área.
Essa
propriedade é muito particular para regiões do tipo .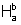
Vamos verificar apenas que ela é completamente razoável, sem fazer uma
demonstração
muito rigorosa.
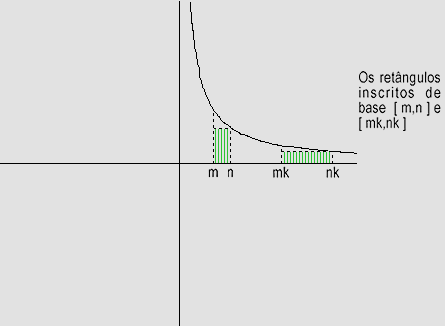
Para tanto, observemos primeiramente o seguinte fato: dado um retângulo
inscrit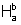o em ,
cuja base é o intervalo [m,n], podemos construir um retângulo cuja base
é [mk,nk] que está inscrito em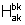 
e que tem a mesma área que o primeiro. Com efeito, a área do primeiro
é
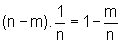
enquanto que a área do segundo é
(nk-mk).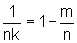
e, portanto, igual à do anterior.
Logo,
quando consideramos retângulos inscritos em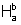
podemos encontrar retângulos inscritos em
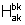com mesma área que os anteriores. Evidentemente o mesmo vale se consideramos
retângulos
circunscritos.
Assim
sendo, a soma das áreas dos retângulos inscritos (circunscritos) em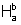
é igual à soma das áreas dos retângulos inscritos (circunscritos) em .
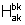Logo
é razoável que as regiões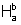
e 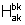tenham a mesma
área. A demonstração
rigorosa desse fato pode ser feita usando a integral
definida.
Conseqüência:
Se a>1 e b>1, então, usando o fato geometricamente evidente que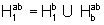 
e a propriedade fundamental, temos que:
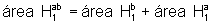
pois
.
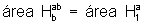Dessa
forma, se definimos uma função f, que a cada x>1, associa a área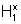 
,
temos que f satisfaz a seguinte propriedade:
f(ab)=f(a)+f(b) para todo a>1 e todo b>1.
A
pergunta que surge é a seguinte: uma vez que estamos considerando regiões
que estão compreendidas entre o eixo x e o ramo positivo do gráfico de
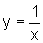, será possível
estender a função f para todo o intervalo ]0,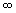
[,
ou seja, definir uma nova função g, que coincida com f em ]1,[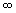
e que conserve a propriedade g(ab)=g(a)+g(b)
também no intervalo ]0,1]?
A resposta é, de fato, afirmativa.
Para mostrar que g existe, vamos exibir uma candidata e mostrar que ela funciona.
Em primeiro lugar, como g(ab)=g(a)+g(b), temos que g(1)=0.
Em
segundo lugar, se 0<a<1, temos, evidentement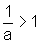e, 
e
Assim, a candidata g verifica:
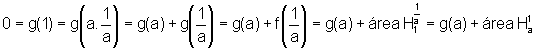
Logo, para o número a, tal que 0<a<1, temos que
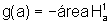
Vamos, então, definir a função g:
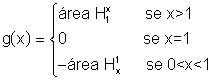
Pela maneira como g foi definida, ela é, evidentemente, uma extensão da função f. Qualquer outra extensão de f obedecendo às mesmas propriedades que g, coincide com g.
A função g verifica a propriedade fundamental g(ab)=g(a)+g(b), para todos os valores estritamente positivos de a e b.
Conclusão: Existe assim uma única função g, que estende a função f inicial e que verifica g(ab)=g(a)+g(b), para todos os valores estritamente positivos de a e b.
Definição:
A função g construída é denominada função ln e é a função definida em
]0,[ dada por
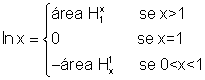
e essa função tem a propriedade ln(ab)=ln(a)+ln(b), para todos a>0 e b>0.
Podemos finalmente, observar que:
ln(x)>0
se, e somente se, x >1;
ln(x)=0 se, e somente se, x=1;
ln(x)<0 se, e somente se,
A função ln é bijetora e, portanto, dado o número real 1, existe um único real x, estritamente positivo, tal que ln x=1. Esse número, por definição, é o número e.
 |
 |