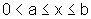g)
a função ln é estritamente crescente, isto é, se a>b>0, então 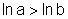 .
.
Observações:
Da
afirmação g) concluímos que g é uma função injetora, isto é, se a>0, b>0
e a 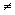 b, então ln a
b, então ln a 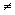 ln b.
ln b.
É
possível provar que a função ln é sobrejetora sobre R, isto é, dado 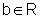 qualquer, sempre existe a>0, único neste caso, tal que ln(a)=b - ver no
livro Logaritmos de autoria de Elon Lages Lima - IMPA-VITAE.
qualquer, sempre existe a>0, único neste caso, tal que ln(a)=b - ver no
livro Logaritmos de autoria de Elon Lages Lima - IMPA-VITAE.
![]() Sendo ln 4 =1,3862 e ln 3 =1,0986, determine, utilizando as propriedades
do ln, os valores aproximados de:
Sendo ln 4 =1,3862 e ln 3 =1,0986, determine, utilizando as propriedades
do ln, os valores aproximados de:
a)
ln 16
b) ln 6
c) ln 288
d) ln 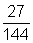
e) ln (1,333…)
f) ln 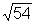
g) ln 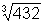
![]() Diga se as afirmações abaixo são verdadeiras ou falsas. Justifique cuidadosamente.
Diga se as afirmações abaixo são verdadeiras ou falsas. Justifique cuidadosamente.
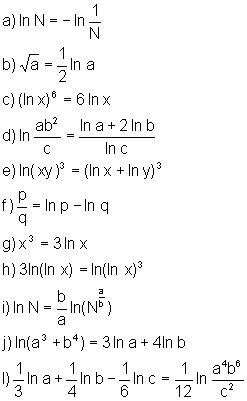
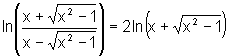
![]() a) Mostre que, para todo x>0 e para todo h>-x, h
a) Mostre que, para todo x>0 e para todo h>-x, h 0,
h racional, tem-se:
0,
h racional, tem-se:

b) Usando a definição de ln por área, mostre que:
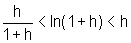 ,
para todo h>0
,
para todo h>0
Por
que podemos afirmar que se h for um número positivo muito próximo de zero,
valerá que 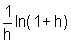 fica próximo de 1?
fica próximo de 1?
a) usando a definição de ln, prove que
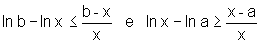
Sugestão: Considere os diferentes casos:
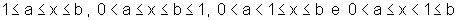
b) Usando a) conclua que
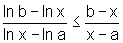
c) Usando b) conclua que
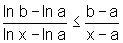
![]() Uma
função , definida num intervalo I, chama-se côncava em I, quando para
quaisquer pontos a,b pertencentes a I, com a<b, tem-se:
Uma
função , definida num intervalo I, chama-se côncava em I, quando para
quaisquer pontos a,b pertencentes a I, com a<b, tem-se:
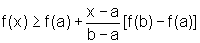 ,
para todo x pertencente ao intervalo [a,b].
,
para todo x pertencente ao intervalo [a,b].
a)Dados a e b em I, com a<b, seja r a reta que passa por (a,f(a)) e (b,f(b)). Escreva a equação de r e interprete geometricamente a desigualdade acima.
b) Prove que a função ln é côncava.
![]() Justifique
a seguinte propriedade dos logaritmos:
Justifique
a seguinte propriedade dos logaritmos:
Mudança
de base: para todos a e b estritamente positivos, sendo
b diferente de 1, temos: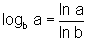 .
.
 |
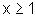 ,
tem-se
,
tem-se