A
área da região 
Consideremos
a hipérbole 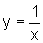 e
o ramo positivo de seu gráfico, isto é o trecho do gráfico determinado
pelos valores reais e positivos de x.
e
o ramo positivo de seu gráfico, isto é o trecho do gráfico determinado
pelos valores reais e positivos de x.
Vamos
estabelecer um procedimento para calcular a área sob o gráfico de 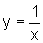 para
para 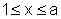 e acima
do eixo x. Estamos denotando essa região por
e acima
do eixo x. Estamos denotando essa região por 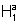 .
.
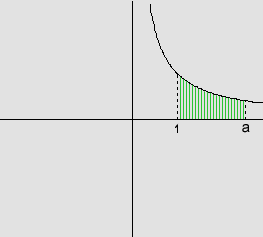
A região
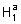
Para
calcular a área de 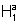 ,
consideramos uma partição do intervalo [1,a], isto é, um conjunto finito
e qualquer de pontos que subdividem o referido intervalo em sub-intervalos.
Em cada sub-intervalo [m,n] do intervalo [1,a], consideramos o retângulo
inscrito em
,
consideramos uma partição do intervalo [1,a], isto é, um conjunto finito
e qualquer de pontos que subdividem o referido intervalo em sub-intervalos.
Em cada sub-intervalo [m,n] do intervalo [1,a], consideramos o retângulo
inscrito em 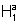 ,
cuja base tem comprimento n-m e cuja altura é
,
cuja base tem comprimento n-m e cuja altura é 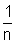 .
.
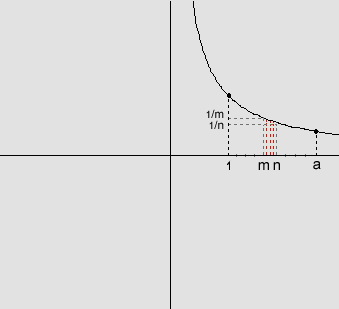
O retângulo
cuja base mede n-m e cuja altura mede 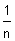
A
soma das áreas dos retângulos desse tipo será utilizada para obter uma
aproximação por falta da área de 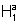 .
.
A
aproximação será tanto melhor quanto mais fina for a partição do intervalo
[1,a]; ou seja, quanto mais pontos estiverem sendo considerados na subdivisão
do intervalo dado, menor será a diferença entre o "valor exato da área
de 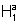 " e a soma das áreas dos retângulos inscritos.
" e a soma das áreas dos retângulos inscritos.
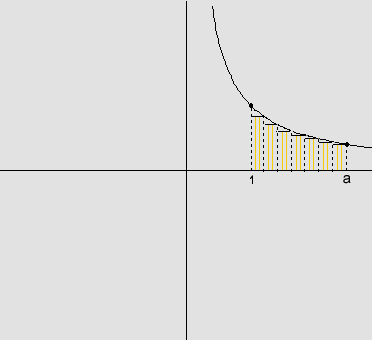
A área
de 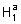 aproximado por falta
aproximado por falta
O
"valor exato da área de 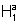 " é o limite
da soma das áreas dos retângulos inscritos quando o número deles tende
a infinito, isto é, quando o número de pontos da partição tende a infinito,
ou ainda quando o comprimento do maior dos sub-intervalos tende a zero.
" é o limite
da soma das áreas dos retângulos inscritos quando o número deles tende
a infinito, isto é, quando o número de pontos da partição tende a infinito,
ou ainda quando o comprimento do maior dos sub-intervalos tende a zero.
É
preciso observar que um raciocínio análogo poderia ter sido desenvolvido
a partir das áreas dos retângulos obtidos ao considerar a base de medida
n-m e altura 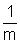 .
Nesse caso, ao calcular a soma das áreas de retângulos considerados dessa
maneira, estaríamos calculando uma aproximação por excesso da área da
região.
.
Nesse caso, ao calcular a soma das áreas de retângulos considerados dessa
maneira, estaríamos calculando uma aproximação por excesso da área da
região.
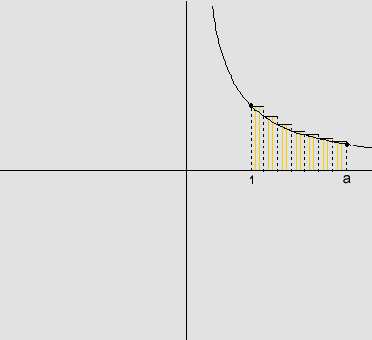
A área
de 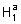 aproximado por excesso
aproximado por excesso
As
áreas das regiões que estamos considerando, isto é, as regiões do tipo
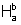 gozam de uma
propriedade
fundamental, que nos permitirá obter uma caracterização interessante
para elas, e definir a
função logarítmica y=ln x.
gozam de uma
propriedade
fundamental, que nos permitirá obter uma caracterização interessante
para elas, e definir a
função logarítmica y=ln x.

