![]() Considerando
a região
Considerando
a região 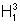 ,
determine uma aproximação para sua área através da partição do intervalo
[1,3] pelos pontos: 1,
,
determine uma aproximação para sua área através da partição do intervalo
[1,3] pelos pontos: 1, 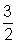 ,
2,
,
2, 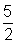 ,
3.
,
3.
![]() Melhore a aproximação obtida no Exercício
1, através de uma partição mais fina do intervalo [1,3], dada por:
1,
Melhore a aproximação obtida no Exercício
1, através de uma partição mais fina do intervalo [1,3], dada por:
1, 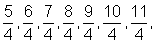 3.
3.
![]() Dado
o intervalo [1,4], considere duas partições, dividindo o intervalo primeiramente
em 6 partes iguais e depois em 12 partes iguais. Em cada uma das situações,
calcule a soma das áreas dos retângulos inscritos, relativos a essas duas
subdivisões, ou seja, calcule duas aproximações por falta de
Dado
o intervalo [1,4], considere duas partições, dividindo o intervalo primeiramente
em 6 partes iguais e depois em 12 partes iguais. Em cada uma das situações,
calcule a soma das áreas dos retângulos inscritos, relativos a essas duas
subdivisões, ou seja, calcule duas aproximações por falta de 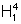 .
.
![]() Calcule, para as partições de [1,4] consideradas no Exercício
3, duas aproximações por excesso para a área de
Calcule, para as partições de [1,4] consideradas no Exercício
3, duas aproximações por excesso para a área de 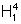 .
.
![]() A
partir do Exercício
3 e Exercício
4, exiba dois números M e N tais que
A
partir do Exercício
3 e Exercício
4, exiba dois números M e N tais que 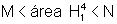 .
.
