A função logaritmo natural mais simples é a função y=f₀(x)=lnx. Cada ponto do gráfico é da forma (x, lnx) pois a ordenada é sempre igual ao logaritmo natural da abscissa.

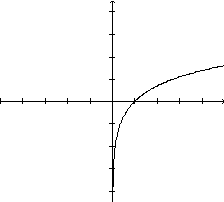
O domínio da função ln é 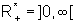e a imagem é o conjunto .
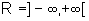O eixo vertical é uma assíntota ao gráfico da função.

O que queremos aqui é descobrir como é o gráfico de uma função logarítmica natural geral, quando comparado ao gráfico de y=ln x, a partir das transformações sofridas por esta função.

Consideremos uma função logarítmica cuja expressão é dada por y=f₁(x)=ln x+k, onde k é uma constante real. A pergunta natural a ser feita é: qual a ação da constante k no gráfico dessa nova função quando comparado ao gráfico da função inicial y=f₀(x)=ln x ?

Ainda podemos pensar numa função logarítmica que seja dada pela expressão y=f₂(x)=a.ln x onde a é uma constante real, a 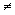0. Observe que se a=0, a função obtida não será logarítmica, pois será a constante real nula.

Uma questão que ainda se coloca é a consideração de funções logarítmicas do tipo y=f₃(x)=ln(x+m), onde m é um número real não nulo.

Se g(x)=3.ln(x-2)+ 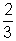, desenhe seu gráfico, fazendo os gráficos intermediários, todos num mesmo par de eixos.

y=a.ln(x+m)+k

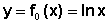Conclusão: Podemos, portanto, considerar funções logarítmicas do tipo , onde o coeficiente a não é zero, examinando as transformações do gráfico da função mais simples , quando fazemos, em primeiro lugar, y=ln(x+m); em seguida, y=a.ln(x+m) e, finalmente, y=a.ln(x+m)+k.

Analisemos o que aconteceu:

• em primeiro lugar, y=ln(x+m) sofreu uma translação horizontal de -m unidades, pois x=-m exerce o papel que x=0 exercia em y=ln x;
• a seguir, no gráfico de y=a.ln(x+m) ocorreu mudança de inclinação pois, em cada ponto, a ordenada é igual àquela do ponto de mesma abscissa em y=ln(x+m) multiplicada pelo coeficiente a;
• por fim, o gráfico de y=a.ln(x+m)+k sofreu uma translação vertical de k unidades, pois, para cada abscissa, as ordenadas dos pontos do gráfico de y=a.ln(x+m)+k ficaram acrescidas de k, quando comparadas às ordenadas dos pontos do gráfico de y=a.ln(x+m).
  
  

O estudo dos gráficos das funções envolvidas auxilia na resolução de equações ou inequações, pois as operações algébricas a serem realizadas adquirem um significado que é visível nos gráficos das funções esboçados no mesmo referencial cartesiano.