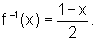A idéia de operação é muito
antiga. Os babilônios já tinham a noção de raiz quadrada e raiz cúbica
e conheciam um algoritmo para a determinação das raízes quadrada ou cúbica
de um número, embora não distinguissem valor aproximado de valor exato
com algum tipo de rigor.
Com os gregos, a Matemática passou a ser encarada como uma ciência dedutiva,
começando a fincar estacas para constituir um conjunto articulado de conceitos
e técnicas. Nesse aspecto, na Geometria, Os
Elementos de Euclides, tiveram um papel fundamental.
Os gregos, em relação à operação inversa de radiciação, faziam distinção
clara entre valor exato e valor aproximado em seus cálculos.
Por volta do século XIV, começou a germinar a idéia de função. Com Euler
e Lagrange
- século XVIII - a idéia em vigor era a de que uma função era aquilo que
tem uma expressão algébrica; em geral, as funções que eles consideravam
eram contínuas
e deriváveis.
Somente com Fourier,
no século XIX, apareceram funções "esquisitas", não necessariamente contínuas.
Foi nessa época que o conceito de função ficou estabelecido. A sistematização,
para se chegar à definição atual de função, ocorreu ainda no século XIX,
com Dirichlet.
Aí também surgiu o conceito de função inversível.
![]() Dada a função
Dada a função 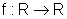 ,
f(x)=x3,
,
f(x)=x3,
observamos que f é inversível e que sua inversa é 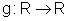 , g(x)=
, g(x)= 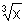 .
.
 Dada a função
Dada a função 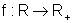 , f(x)=x2, observamos que, neste caso,
f não é inversível, ou seja, não existe a função inversa de f.
, f(x)=x2, observamos que, neste caso,
f não é inversível, ou seja, não existe a função inversa de f.
 A função
A função 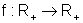 ,
f(x)=x2, é inversível e sua inversa é
,
f(x)=x2, é inversível e sua inversa é
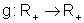 ,
, 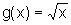 .
.
![]() Também
a função
Também
a função 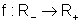 ,
,
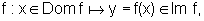 f(x)=x2,
admite inversa
f(x)=x2,
admite inversa 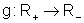 ,
,
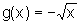 .
.
Uma consideração importante faz-se necessária.
Vimos na Situação 2, que a função f(x)=x2
com Dom f=R e Im f=R+ não é inversível. Entretanto, considerando
a função
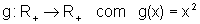
conforme a Situação 3, temos
que esta é inversível, com inversa 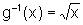 .
.
Analogamente, podemos considerar
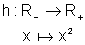
que também é inversível,
com inversa 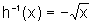 ,
conforme Situação 4.
,
conforme Situação 4.
É preciso ficar claro que,
dada uma função 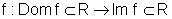 ,
se ela não for inversível, é possível restringir o domínio de tal modo
que a função definida nesse novo domínio seja inversível. Normalmente,
ao considerar a função restrita a um subconjunto do domínio inicial, denotamo-la
de uma forma um pouco mais complicada; no exemplo acima:
,
se ela não for inversível, é possível restringir o domínio de tal modo
que a função definida nesse novo domínio seja inversível. Normalmente,
ao considerar a função restrita a um subconjunto do domínio inicial, denotamo-la
de uma forma um pouco mais complicada; no exemplo acima: 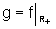 e
e 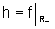 , que se
lêem, respectivamente, "f restrita a R+" e "f restrita a R-".
, que se
lêem, respectivamente, "f restrita a R+" e "f restrita a R-".
Façamos agora outras considerações. Em todos as situações vistas, os gráficos de uma função e de sua inversa apresentaram uma característica importante, qual seja, em cada caso, a simetria em relação à bissetriz do primeiro e terceiro quadrantes, ou seja em relação à reta y=x.
Este fato é natural e ocorre sempre, pois, sendo f inversível, a
sua inversa f-1, a cada número real da imagem
de f deve associar o número x do domínio
de f , isto é,
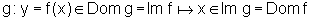 .
.
Assim, se o par ordenado (x,f(x)) está no gráfico de f, o par ordenado (f(x),x) estará no gráfico de g. Esses pares ordenados são pontos simétricos em relação à reta que contém as bissetrizes do primeiro e terceiro quadrantes.
Após a análise das situações e as considerações realizadas, podemos estabelecer as seguintes conclusões:
i) Se uma função f admite
uma inversa g, então g também admite uma inversa que é a própria f.
ii) Dada uma função dizemos que ela é inversível quando podemos determinar
uma outra função que "desfaz o serviço de f", isto é, tal que
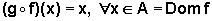
e
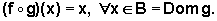
Nesse caso, g é denominada
a função inversa de f e, portanto, f é a inversa de g. Normalmente, a
função inversa de f é denotada por 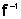 .
.
iii) Para uma função f ser inversível,
é suficiente que a função seja estritamente crescente ou estritamente
decrescente em seu domínio. Isso significa que ela deve ser bijetora
sobre a imagem.
 Verifiquemos
que a inversa de f(x) = 1 - 2x é a função
Verifiquemos
que a inversa de f(x) = 1 - 2x é a função 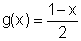 .
.
Uma pergunta natural é a seguinte: dada uma função f, como fazemos, na prática, para determinar sua inversa?
Vejamos: se temos a função f, significa que para cada valor da variável independente x obtemos, em correspondência, um valor para a variável dependente y.
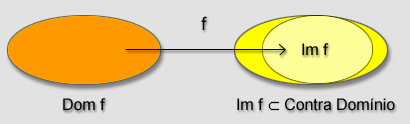
Ao procurar a inversa de f pretendemos encontrar a função g que, a cada y na imagem de f associa o x inicial no domínio de f .
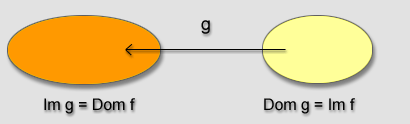
No caso da Situação 5, a função foi dada por y=f(x)=1-2x.
Assim, podemos escrever
que 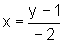 , ou seja,
, ou seja,
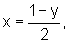 que nos fornece
a variável x na dependência de y.
que nos fornece
a variável x na dependência de y.
Como, normalmente, denotamos a variável independente pela letra x, escrevemos
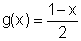 ou também
ou também