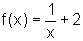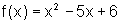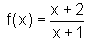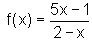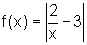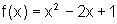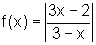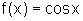![]() Mostre que a condição não é necessária, isto é, a função ser inversível não implica que ela seja estritamente crescente ou estritamente decrescente.
Mostre que a condição não é necessária, isto é, a função ser inversível não implica que ela seja estritamente crescente ou estritamente decrescente.
![]() Dadas as funções abaixo,
determine para cada uma a sua inversa. Represente graficamente, em cada
caso, a função e sua inversa, num mesmo par de eixos.
Dadas as funções abaixo,
determine para cada uma a sua inversa. Represente graficamente, em cada
caso, a função e sua inversa, num mesmo par de eixos.
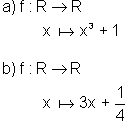
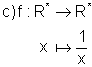
![]() Mostre, utilizando
argumentos de geometria plana, que os pares ordenados (a,b) e (b,a) são
simétricos em relação à reta y=x.
Mostre, utilizando
argumentos de geometria plana, que os pares ordenados (a,b) e (b,a) são
simétricos em relação à reta y=x.
![]() Em cada caso, a função
dada abaixo por seu gráfico, é inversível? Em caso afirmativo, represente,
no mesmo par de eixos, o gráfico da inversa. Em caso negativo, justifique
a não existência da inversa.
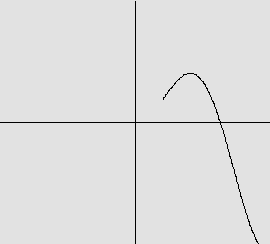
Em cada caso, a função
dada abaixo por seu gráfico, é inversível? Em caso afirmativo, represente,
no mesmo par de eixos, o gráfico da inversa. Em caso negativo, justifique
a não existência da inversa.
a)
b) 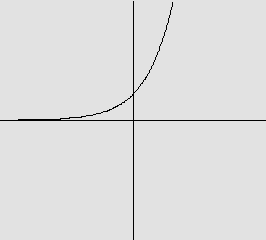
c)
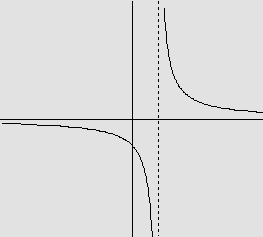
d)
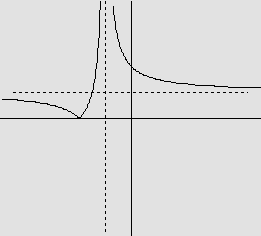
 Dadas as funções abaixo,
para cada uma esboce o gráfico, decida se é inversível e, nesse caso,
dê a expressão da inversa e o seu gráfico, no mesmo par de eixos do que
a função inicial. Caso a função não seja inversível, restrinja o domínio
a fim de obter uma função inversível; a seguir, proceda como acima.
Dadas as funções abaixo,
para cada uma esboce o gráfico, decida se é inversível e, nesse caso,
dê a expressão da inversa e o seu gráfico, no mesmo par de eixos do que
a função inicial. Caso a função não seja inversível, restrinja o domínio
a fim de obter uma função inversível; a seguir, proceda como acima.