Algumas vezes nos defrontamos com afirmações envolvendo os números naturais e a questão que surge é: será tal afirmação verdadeira sempre, ou seja, vale para qualquer número natural?

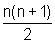1+2+...+n= , para todo número natural .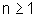

1+q+q²+...+qⁿ=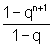 , para todo número natural n.

A igualdade (n+1).(n-1)+[(n-1).(n-2)...(n-1000)]=n²-1 vale para todo número natural?

A soma dos n primeiros números ímpares é n².

É claro que para responder às questões colocadas pelos problemas não basta "testar" a veracidade das "fórmulas" substituindo valores específicos para n. Por mais que as igualdades ganhem credibilidade, nunca poderemos estar garantindo sua validade para algum valor de n que não tenha sido testado!

Segundo Simmons, há um abismo entre "provavelmente verdadeira" e "absolutamente certa". É necessário um argumento lógico garantindo que uma certa propriedade envolvendo os números naturais seja sempre verdadeira para todos os valores de n, para eliminar qualquer dúvida. Isto é o que realiza o método de demonstração por indução matemática.

Algumas vezes, temos argumentos para verificar a veracidade de uma tal afirmação. Outras vezes, fazemos uso de um Teorema que nos fornece um método para demonstrar igualdades, desigualdades, ou, de modo mais geral, propriedades que dependem de números naturais.

Esse Teorema é conhecido como o Princípio da Indução Finita - P.I.F. - cujo enunciado é o seguinte:

Princípio da Indução Finita:

Seja P(n) uma propriedade descrita em termos de números naturais n. Suponhamos que as afirmações abaixo estejam satisfeitas:

a) P(1) é válida.
b) Se P(k) vale então P(k+1) também vale.

Nesse caso então P(n) é válida para todo .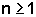

O P.I.F., intuitivamente, nos garante que se tivermos um conjunto finito de, por exemplo, peças de dominó dispostas verticalmente, de tal modo que quando uma cai, a seguinte cai - e sendo dado que a primeira cai - concluímos que todas caem. Evidentemente, não importa quantas peças tenhamos em nosso conjunto...

Provar a veracidade de uma dada afirmação, utilizando o Princípio da Indução Finita, significa, em comparação à situação das peças do dominó, mostrar que todas as peças caem. Para tanto, pelo Teorema, basta mostrar que a primeira cai e que, quando uma qualquer cai, a seguinte cai.