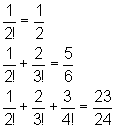Utilizando o P.I.F., demonstre as seguintes propriedades:

a) 1+2+...+n=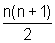
b) 1+q+q²+...+qⁿ=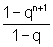
c) Para todo a>0, ln aⁿ=n.ln a
d) O binômio de Newton: 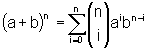, onde é denominado número binomial.
e)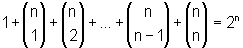
f) 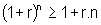, para todo r >0
g) 1+3+5+...+(2n-1)=n²

Calcule as seguintes somas - isto é, encontre em cada caso, uma "fórmula":

a) 2+4+6+...+2n
b) 3+8+13+...+(5n-2)

a) Encontre uma "fórmula" que forneça a soma dos quadrados dos n primeiros números naturais.
Sugestão: Observe que para cada k natural, tem-se
(k+1)³-k³=3k²+3k+1.
Some então, membro a membro, as igualdades acima, fazendo k variar de 1 a n.

b) Encontre uma "fórmula" que forneça a soma dos cubos dos n primeiros números naturais.
Outra solução: há uma bela solução geométrica em Simmons, volume 1, pág. 766.

Seja P(n) a seguinte afirmação: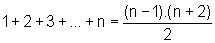

a) Mostre que, se P(k) vale, então P(k+1) também vale.
b) Podemos concluir que P(n) é válida para todo n?

Observe que a desigualdade 2ⁿ>3n não é válida para n=1. Na realidade, o primeiro natural para o qual 2ⁿ>3n é n=4. Enuncie um P.I.F. que possa ser utilizado para demonstrar que 2ⁿ>3n para todo .

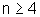Descubra a lei sugerida pelos fatos apresentados e prove-a por indução: