![]()
a)Seja S=12+22+32+...+k2 a soma procurada.
Consideremos a expansão
(k+1)3=k3+3k2+3k+1,
de onde podemos escrever:
(k+1)3-k3=3k2+3k+1.
Fazendo k variar de 1 a n, obtemos as seguintes identidades:
| k=1: |
23-13=3.12+3.1+1
|
| k=2: | 33-23=3.22+3.2+1 |
| k=3: | 43-33=3.32+3.3+1 |
.......................................................................
| k=n-1: |
n3-(n-1)3=3.(n-1)2+3.(n-1)+1
|
| k=n: | (n+1)3-n3=3.n2+3.n+1 |
Somando todos os primeiros membros e todos os segundos membros, e fazendo os cancelamentos, obtemos:
(n+1)3-13=3.(12+22+32+...+n2)+3(1+2+3+...+n)+n
ou seja
(n+1)3-13=3.S+
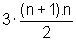 +n,
+n,
pois usamos o resultado obtido na Situação 1.
Logo, o valor procurado para S é dado por:
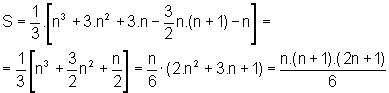
Logo, a soma dos quadrados dos n primeiros números naturais é dada por:
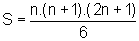
b) Seja S=13+23+33+...+k3
a soma procurada.
Consideremos, agora, a expansão
(k+1)4=k4+4k3+6k2+4k+1,
de onde podemos escrever:
(k+1)4-k4=4k3+6k2+4k+1
Fazendo k variar de 1 a n, obtemos as seguintes identidades:
| k=1: |
24-14=4.13+6.12+4.1+1
|
| k=2: | 34-24=4.23+6.22+4.2+1 |
| k=3: | 44-34=4.33+6.32+4.3+1 |
.........................................................................................................
| k=(n-1): |
n4-(n-1)4=4.(n-1)3+6.(n-1)2+4.(n-1)+1
|
| k=n: | (n+1)4-n4=4.n3+6.n2+4.n+1 |
Fazendo os cancelamentos encontrados, obtemos:
(n+1)4-14=4.(13+23+33+...+n3)+6.(12+22+32+...+n2)+4.(1+2+3+...+n)+n
ou seja
(n+1)4-14=4.S+
 +n,
+n,
pois usamos o resultado anterior e aquele obtido na Situação 1.
Logo, o valor procurado para S é dado por:
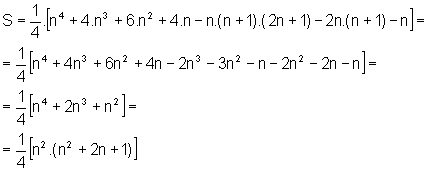
ou seja,
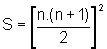 .
.
