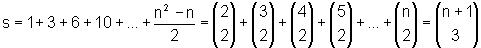Outra solução para o cálculo da soma dos quadrados dos primeiros n números naturais:

.

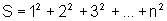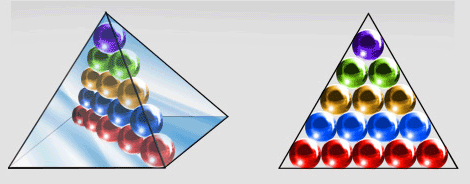
Consideremos uma "pirâmide" de bolinhas, dispostas da seguinte maneira:

• em cima uma única bolinha;
• logo abaixo, 4 bolinhas;
• abaixo, 9 bolinhas;
• abaixo, 16;
• abaixo, 25;
• ........
• na parte mais abaixo de todas, n² bolinhas.

É claro que o nosso objetivo é o de contar quantas bolinhas existem, ou seja, calcular .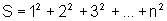

Para tanto, vamos considerar que o conjunto todo foi dividido em três partes, considerando a "diagonal":

• a primeira parte é constituída pelas bolinhas que estão na "diagonal": o total delas é 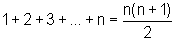, conforme vimos na Situação 1.
• as outras duas partes, obtidas ao retirar as bolinhas que estão na diagonal têm a mesma quantidade e o número de bolinhas em cada uma delas, pode ser obtido observando que temos:

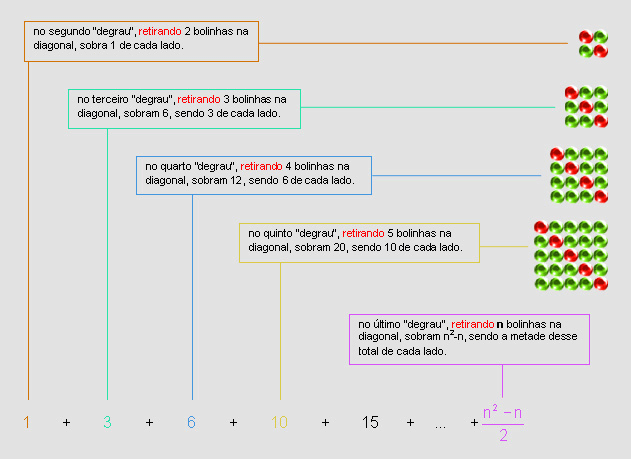
Assim cada uma dessas partes tem um total de bolinhas que é o resultado da soma de: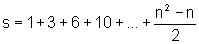

.

Um fato a ser percebido é que 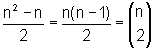e, com isso, examinando o Triângulo de Pascal, descobrimos a seqüência de números, cuja soma queremos calcular. Essa sequência constitui sua terceira coluna.

Assim,

Logo,

.

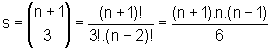
Finalmente, a soma das bolinhas existente na "pirâmide" é:
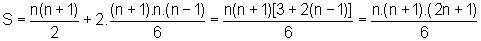