Nosso objetivo é tentar explicitar algumas noções sobre a linguagem matemática e o raciocínio lógico utilizados nos textos matemáticos.

A linguagem matemática não é aquela utilizada no dia a dia, quando nos expressamos através de algum idioma, seja ele português, inglês, italiano, espanhol,... Basta comparar um texto matemático com um texto literário, para percebermos a diferença. E não se trata apenas de uma questão de simbologia; a questão fundamental reside na lógica interna da linguagem matemática que é diferente daquela da língua materna.

Em Matemática, todas as palavras têm um sentido preciso. Isso significa que o conhecimento do significado das palavras é fundamental.

1. A linguagem proposicional

Uma oração ou frase em Matemática pode estar afirmando um fato correto - isto é, verdadeiro (V) - ou errado - isto é, falso (F) -. A partir de frases, verdadeiras ou falsas, podemos formar outras frases usando expressões como: "... e ...", "... ou ...", "não...", "se ... então ...", "... se, e somente se, ...", "... sempre que ...", "... equivalente a ...", "... portanto ...", e assim por diante.

A fim de facilitar o entendimento, vamos denotar uma frase qualquer por uma letra minúscula do alfabeto: p, q, r, s, etc.

A veracidade ou falsidade de uma proposição que envolve alguma das expressões acima - isto é, uma proposição composta - pode ser concluída através da chamada tabela-verdade, que é construída a partir da combinação dos valores V ou F das proposições básicas, que compõem a frase.

A negação: Dada uma frase p, que pode ser V ou F, sua negação - que se indica por "~p" - será, respectivamente F ou V.

A conjunção "... e ...": Dadas duas frases p e q, que podem ser V ou F, a frase "p e q" - que também é indicada por "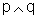 " - será V apenas quando cada uma das frases iniciais for V.

A disjunção "... ou ...": Dadas duas frases p e q, que podem ser V ou F, a frase "p ou q" - que também é indicada por " 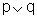" - será F apenas quando cada uma das frases iniciais for F.

A implicação "se ... então ...": Dadas duas frases p e q, que podem ser V ou F, a frase "se p então q" - que também é indicada por " 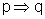" - será F apenas no caso em que p é V e q é F.

A equivalência "...se e somente se...": Dadas duas frases p e q, que podem ser V ou F, a frase "p se e somente se q" ou "p é equivalente a q" - que também é indicada por " " - será verdadeira quando ambas forem verdadeiras ou ambas forem falsas.

2. A quantificação

Em Matemática utilizam-se dois quantificadores: o existe e o para todo, que são denotados, respectivamente por .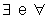

A expressão "existe" 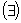é utilizada quando a propriedade enunciada admite pelo menos um elemento no universo considerado que a verifica.

Encontramos situações em que aparece a expressão "existe um único" 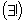ou "existe e é único".

A expressão "para todo" 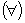é utilizada quando a propriedade enunciada é verdadeira para "qualquer que seja" o elemento no universo considerado.

Se p é a proposição: 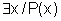, isto é, "existe x tal que x verifica a propriedade P", a negação do "existe" significa que a propriedade enunciada não é satisfeita "para todo" elemento do universo em questão. Ou seja, qualquer elemento do universo considerado não satisfaz a propriedade P. Por exemplo,

se p: existe x tal que x<4,

então ~p: qualquer que seja x, .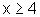

Por outro lado, se q é a proposiçã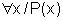o: , isto é, "qualquer que seja x, x verifica a propriedade P", a negação do "para todo" significa que "existe" algum elemento no universo que não satisfaz a propriedade em questão. Ou seja, existe pelo menos um elemento no universo que não verifica a propriedade P. Por exemplo,

se q: para todo x, 2x=0

então ~q: existe x tal que .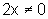

3. Teoremas e demonstrações

Essencialmente, todos os resultados da matemática - ou seja, as afirmações que podem ser chamadas teoremas, ou proposições, ou mesmo lemas - são da forma hipótese(s) implica(m) tese. Dito de outra maneira, os resultados são da forma: partindo de alguns pressupostos - hipóteses - podemos concluir a tese.

O processo de demonstração de um resultado é realizado a partir dessas hipóteses e, mediante raciocínios mais ou menos elementares, onde vão sendo obtidas conclusões intermediárias, até se chegar à conclusão desejada.
Uma demonstração é uma lista de evidências de que a afirmação do teorema é verdadeira.