Conforme vimos nos exemplos de Taxa de Variação Média, as informações dadas por ela são relativamente pobres quando estamos interessados em conhecer o comportamento de uma função.

A fim de alcançar esse objetivo, seria interessante conhecer a taxa de variação em intervalos de comprimento "muito pequeno" o que ainda não resolveria o nosso problema, uma vez que "muito pequeno" não é algo totalmente claro. O ideal mesmo seria conseguir definir o que é taxa de variação em cada ponto.

A questão é: como definir a velocidade instantânea de um corpo em movimento num determinado instante?

Suponhamos que a equação horária do movimento de um corpo é dada por
s(t)=t²+5 e que desejamos saber a velocidade do corpo no instante t=2. Como podemos achar essa velocidade?

Imaginemos que um vaso de flores caiu da janela de um prédio, isto é, temos um corpo em queda livre, cujo movimento iniciou-se de uma altura h. Da Física, sabemos que a equação horária do movimento de um corpo em queda livre, com velocidade inicial nula, é dada por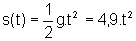
considerando a aceleração da gravidade g=9,8m/s². Intuitivamente, percebemos que a velocidade, em cada instante, aumenta.
Como podemos calcular a velocidade instantânea, por exemplo, 1s após o início da queda? E após 2s?

Suponha que uma bexiga está sendo inflada, produzindo uma esfera perfeita. Qual a taxa de variação pontual do volume de uma esfera de raio r, em função do raio? Com que taxa varia o volume da esfera quando r= 2m?

Observações:
i) a taxa de variação pontual de f no ponto x₀ é denominada simplesmente taxa de variação de f no ponto x₀. No caso da variável independente ser o tempo, a taxa de variação é denominada instantânea.
Quando se trata de taxa de variação média de uma função f num determinado intervalo, a palavra "média" é imprescindível.

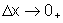ii) dada y=f(x) para calcularmos a taxa de variação pontual de f no ponto x₀, se consideramos o acréscimo Dx>0, fazemos Dx se aproximar de 0 por valores positivos e escrevemos Se consideramos Dx<0, fazemos se aproximar de 0 por valores negativos e escrevemos 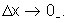Quando, ao calcularmos o limite, escrevemos simplesmente 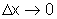, estamos fazendo Dx se aproximar de 0 tanto por valores positivos como negativos.

A taxa de variação pontual ou instantânea de uma função possui uma interpretação geométrica importante que será útil em nosso estudo das funções.