Para calcular a derivada de uma função que seja derivável, em determinado ponto do seu domínio, podemos sempre usar a definição. Entretanto, dependendo da função, isto pode significar bastante trabalho.
Trata-se de uma função polinomial que, em certo sentido, nem é tão complicada. Mas é possível imaginar como ficaria trabalhoso calcular a taxa de variação média dessa função em determinado intervalo, bem como o limite da taxa de variação média...
Outro exemplo
pode ser o da função: 
É fácil ver que, neste caso, calcular a derivada num ponto do domínio, utilizando apenas a definição, é ainda pior...
Esses são exemplos que ilustram situações nas quais conhecer alguns mecanismos teóricos facilita sobremaneira a tarefa.
Felizmente, o problema de encontrar a derivada de uma função satisfaz algumas importantes propriedades que facilitam muito o cálculo no caso de funções obtidas através de operações entre funções mais simples.
Uma vez que tivermos provado as propriedades abaixo, usando a definição de derivada, teremos a possibilidade de calcular derivadas de funções mais complicadas, sem muito trabalho. Vamos lá!
![]() A derivada de uma função constante é zero.
A derivada de uma função constante é zero.
![]() Se
f e g são deriváveis, então f+g
é derivável e
Se
f e g são deriváveis, então f+g
é derivável e 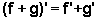 .
.
![]() Se f é derivável e k é uma constante, então
k.f é derivável e
Se f é derivável e k é uma constante, então
k.f é derivável e 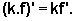
![]() Se f e g são deriváveis, então f.g
é derivável e
Se f e g são deriváveis, então f.g
é derivável e 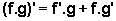 .
.
Observemos que algumas dessas propriedades têm uma
interpretação geométrica muito simples. Por exemplo,
é claro que, em cada ponto, o coeficiente angular da reta tangente
ao gráfico de uma função constante - que é
uma reta horizontal - é zero.
Por outro lado, dada uma função f, quando consideramos a função k.f, onde k é uma constante não nula, mudamos a inclinação do gráfico através do fator k; sendo assim, é natural que o coeficiente angular da reta tangente, em cada ponto, fique multiplicado pelo mesmo k.
Quando somamos duas funções é bastante natural pensar que o coeficiente angular, da reta tangente ao gráfico da função soma, é igual à soma dos coeficientes angulares das retas tangentes aos gráficos das funções parcelas: isso é precisamente o que garante o Teorema 2.
Para a especial operação de composição de duas funções deriváveis, temos uma regra especial para calcular a derivada da função composta, denominada Regra da Cadeia.
