![]()
![]() Encontre a derivada da função y=f(x)=(2x+1)5.
Encontre a derivada da função y=f(x)=(2x+1)5.
Neste caso, o trabalho de expansão é tedioso, mas não é muito difícil, nem tão demorado.
Entretanto se, no caso de y=f(x)=(2x+1)200, utilizarmos o Binômio de Newton para desenvolver (2x+1)200, e em seguida, acharmos a derivada, não parece ser uma boa idéia por ser muito trabalhoso.
Caso alguém se aventurasse a fazer tal desenvolvimento, apresentaríamos um expoente ainda maior, até recebermos uma resposta do tipo: que loucura!!!
A questão é
que a expressão y=f(x)=(2x+1)200 denota uma função
f que pode ser obtida como composição
de duas outras funções, ou seja, 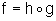 - que significa f(x)=h(g(x)) para todo x real - onde g(x)=2x+1
e h(x)=x200, logo h(g(x))=(2x+1)200.
- que significa f(x)=h(g(x)) para todo x real - onde g(x)=2x+1
e h(x)=x200, logo h(g(x))=(2x+1)200.
Precisamos encontrar uma forma de calcular a derivada da função composta a partir das derivadas das funções componentes.
![]() Considerando
a função y=f(x)=(x3)2, calcule sua
derivada.
Considerando
a função y=f(x)=(x3)2, calcule sua
derivada.
![]() Calcule o produto das derivadas das funções y=h(u)=u2
e u=g(x)=x3. Considerando a função f(x)=h(g(x))=(x3)2,
qual a sua conclusão a respeito da derivada f'?
Calcule o produto das derivadas das funções y=h(u)=u2
e u=g(x)=x3. Considerando a função f(x)=h(g(x))=(x3)2,
qual a sua conclusão a respeito da derivada f'?
![]() Verifique que no exemplo da Situação 1 a conclusão
da Situação 3 é satisfeita.
Verifique que no exemplo da Situação 1 a conclusão
da Situação 3 é satisfeita.
Nessas situações
vimos que se y=h(u) e u=g(x), ou seja, y=h(g(x)), sendo h e g
deriváveis, então a função composta y=h(g(x))
é derivável e
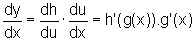
A questão que emerge é a seguinte: será que isso acontece sempre?
A resposta é afirmativa e, intuitivamente, podemos perceber que tal fato é razoável, pois se, em cada ponto, y está variando k vezes em relação a u e u está variando b vezes em relação a x, então y está variando k.b vezes em relação a x.
A propriedade que garante formalmente a veracidade de tal conjectura é conhecida como a Regra da Cadeia, que fornece a derivada da função composta.
Regra
da Cadeia: Sejam y=h(u) e u=g(x) duas funções deriváveis,
com 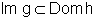 , e consideremos
a função composta y=f(x)=h[g(x)]. Então f é
derivável e f'(x)=h'(g(x)).g'(x), para todo
, e consideremos
a função composta y=f(x)=h[g(x)]. Então f é
derivável e f'(x)=h'(g(x)).g'(x), para todo 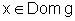 .
.
