![]() Calcule a derivada de cada uma das funções abaixo:
Calcule a derivada de cada uma das funções abaixo:
Assumindo que f e g são deriváveis, encontre a derivada da função p.
Sugestão: Escreva 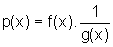 e derive utilizando a regra da derivada
do produto e a Regra
da Cadeia.
e derive utilizando a regra da derivada
do produto e a Regra
da Cadeia.
![]() Encontre a derivada de f(x)=tg x, utilizando o Exercício 2.
Encontre a derivada de f(x)=tg x, utilizando o Exercício 2.
![]() Encontre a derivada de
Encontre a derivada de 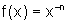 ,
sendo n um número natural.
,
sendo n um número natural.
![]() Sabendo que a velocidade é a derivada da posição
com relação ao tempo e que a aceleração
é a derivada da velocidade com relação ao tempo,
se a aceleração é constante, a posição
deve ser dada por uma função do tempo de qual tipo?
Sabendo que a velocidade é a derivada da posição
com relação ao tempo e que a aceleração
é a derivada da velocidade com relação ao tempo,
se a aceleração é constante, a posição
deve ser dada por uma função do tempo de qual tipo?
![]() Encontre uma função cuja derivada seja
Encontre uma função cuja derivada seja 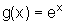 . Em seguida, encontre outra que tenha a mesma derivada. Quantas funções, com essa propriedade, é possível encontrar?
. Em seguida, encontre outra que tenha a mesma derivada. Quantas funções, com essa propriedade, é possível encontrar?
![]() Encontre uma função cuja derivada coincida com ela. Em
seguida, encontre outra função com a mesma propriedade.
Quantas funções, com essa propriedade, é possível
encontrar?
Encontre uma função cuja derivada coincida com ela. Em
seguida, encontre outra função com a mesma propriedade.
Quantas funções, com essa propriedade, é possível
encontrar?
![]() Encontre
a equação da reta tangente e da reta normal ao gráfico
de
Encontre
a equação da reta tangente e da reta normal ao gráfico
de 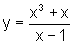 no ponto
de abscissa 2.
no ponto
de abscissa 2.
![]() Da
Física, sabemos que a corrente I, que atravessa um circuito,
é uma função do tempo e é dada por:
Da
Física, sabemos que a corrente I, que atravessa um circuito,
é uma função do tempo e é dada por: 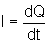 ,
onde a carga Q de um capacitor, que inicia a descarga no instante t=0,
é dada por
,
onde a carga Q de um capacitor, que inicia a descarga no instante t=0,
é dada por
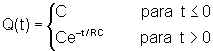
R e C são
constantes positivas que dependem do circuito. Determine a corrente
I, em função do tempo.
![]() Uma
partícula está em um movimento harmônico simples
se a equação do seu movimento é dada pela fórmula
Uma
partícula está em um movimento harmônico simples
se a equação do seu movimento é dada pela fórmula 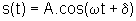 . Encontre a equação
da velocidade dessa partícula.
. Encontre a equação
da velocidade dessa partícula.
![]() Sendo
u uma função de x, isto é, u=u(x), exprima cada
uma das seguintes derivadas em termos de u e de
Sendo
u uma função de x, isto é, u=u(x), exprima cada
uma das seguintes derivadas em termos de u e de 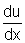 :
:
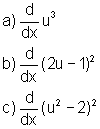
![]() Determine
uma função y=f(x) tal que
Determine
uma função y=f(x) tal que
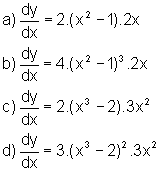
Sua resposta, em cada caso, é única? Justifique.
Observação: Cada uma das equações apresentadas é denominada uma equação diferencial.
![]() Utilizando
a Regra da Cadeia, encontre a derivada das funções abaixo:
Utilizando
a Regra da Cadeia, encontre a derivada das funções abaixo:
a) f(x)=cotg x
b) g(x)=sec x
c) h(x)=cossec x
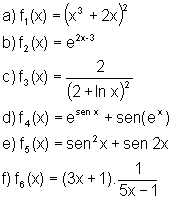
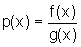 , de modo
tal que
, de modo
tal que 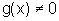 .
.
