A diferencial de uma função e o cálculo aproximado
Sendo f uma função derivável e seja x0 um ponto de seu domínio. Sabemos encontrar a reta tangente ao gráfico de f passando pelo ponto (x0,f(x0)).
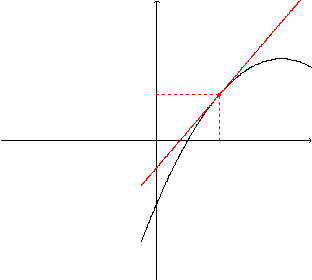
Assim, fixado o ponto (x0,f(x0)), a curva fica muito
perto da reta tangente nas proximidades do ponto de tangência. Isso
significa que para pontos suficientemente próximos de x0
o valor de f(x0) estará próximo do valor da ordenada
do ponto de mesma abscissa x0 mas que se encontra na reta tangente.
Dessa maneira, a derivada de uma função nos permite resolver problemas de cálculos aproximados. Vejamos como.
ln 3 
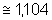
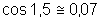
Em todas as situações
acima, observamos que há uma função f envolvida,
que é derivável em um ponto x0 de seu domínio
e tal que f(x0) é um valor conhecido. O problema é
o de determinar o valor de 
para um valor 
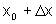"próximo" de x0.
Na figura abaixo, podemos observar uma ampliação da situação geral descrita acima.
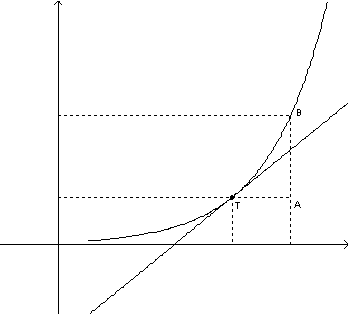
Assim, quando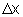 
é "pequeno", obtemos uma aproximação "razoável",
por falta ou por excesso, dependendo do caso, para o valor de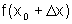 
.
Essa aproximação é dada por:
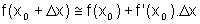
de onde podemos escrever
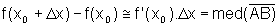
Fixado x, podemos
olhar a função
linear que, a cada 
,
associa 
,
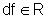onde
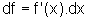
Tal função
é denominada a diferencial de f em x.
 |
 |