![]()
Quando escrevemos y=f(x), estamos dizendo que y é uma função
da variável independente x, explicitando a expressão
da referida função. É o caso, por exemplo, de:
- y=x2
- y=sen x
- y=ln x+3x-4tg x
- e assim por diante...
Podemos estabelecer uma infinidade de funções dessa maneira.
Entretanto, muitas vezes, encontramos equações relacionando as variáveis x e y, nas quais a variável y não está escrita como uma função da variável x, como por exemplo:
- x+y=1
- x2+y2=1
- y+ey-x=2
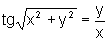
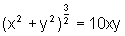
Na primeira equação, conseguimos facilmente explicitar a variável y escrevendo:
y=1-x
Na segunda, temos y2=1-x2, ou seja, podemos escrever:
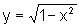 ou
ou 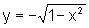 ,
,
isto é, a equação dada fornece duas funções na variável x.
Na terceira e quarta equações simplesmente não conseguimos isolar a variável y e, na última, se possível for, certamente não será muito fácil.
Assim, dada uma equação envolvendo as variáveis x e y, quando conseguimos isolar a variável y, dizemos que y é uma função de x e podemos naturalmente estudá-la. Entretanto, quando não conseguimos isolar y, dizemos que y é uma função implícita de x, ou que a relação dada define y implicitamente como uma função de x.
É talvez surpreendente
que possamos calcular a derivada 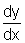 de uma função implícita sem explicitar primeiro a
variável y. Com isso, podemos calcular o coeficiente angular
da reta tangente à curva, mesmo que ela não represente o
gráfico de uma função. Evidentemente, isso só
não será possível se essa reta tangente for uma reta
vertical, pois nesse caso o coeficiente angular não existirá,
pois
não existe
de uma função implícita sem explicitar primeiro a
variável y. Com isso, podemos calcular o coeficiente angular
da reta tangente à curva, mesmo que ela não represente o
gráfico de uma função. Evidentemente, isso só
não será possível se essa reta tangente for uma reta
vertical, pois nesse caso o coeficiente angular não existirá,
pois
não existe 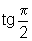 .
.
No caso, por exemplo, de uma equação polinomial nas variáveis x e y podemos, muitas vezes, desenhar uma curva plana como o conjunto de pontos (x,y) que satisfazem a referida equação. O cálculo da derivada da função implícita y em determinado ponto x0, nos permite encontrar o coeficiente angular da reta tangente à curva no ponto - ou nos pontos - de abscissa x0.
![]() Se x2+y2=1, então derivando implicitamente,
considerando que y=y(x), encontramos
Se x2+y2=1, então derivando implicitamente,
considerando que y=y(x), encontramos 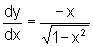 se y>0 ou
se y>0 ou 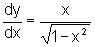 se y<0.
se y<0.
![]() Se
Se 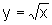 , então
, então
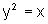 e, derivando
implicitamente, chegamos ao resultado conhecido
e, derivando
implicitamente, chegamos ao resultado conhecido 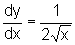 ,
para x>0.
,
para x>0.
![]() Usando derivação implícita, sendo
Usando derivação implícita, sendo  ,
com x>0, encontramos que
,
com x>0, encontramos que 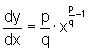
![]() Usando derivação implícita, sendo y(x)=arcsen x,
encontramos que
Usando derivação implícita, sendo y(x)=arcsen x,
encontramos que 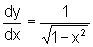 ,
para
,
para 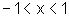 .
.
![]() Usando derivação implícita, sendo y(x)=arctg x, encontramos
que
Usando derivação implícita, sendo y(x)=arctg x, encontramos
que 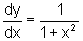 , para
todo
, para
todo 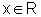 .
.
![]() De modo geral, se f é uma função inversível,
derivável, com derivada não nula e se sua inversa f-1
é derivável, então
De modo geral, se f é uma função inversível,
derivável, com derivada não nula e se sua inversa f-1
é derivável, então 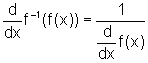 .
.
Enfraquecendo as hipóteses da Situação 6, temos uma propriedade mais geral, que é o Teorema da Função Inversa.
Teorema
da Função Inversa: Seja f inversível com inversa
f-1. Se f for derivável em
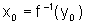 com
com 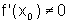 ,
e se f-1 for contínua em
y0, então será derivável
em y0, com
,
e se f-1 for contínua em
y0, então será derivável
em y0, com 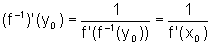 .
.
 |
