![]() Calcule
Calcule 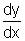 , sendo
y=y(x) uma função dada implicitamente em cada caso por uma
equação:
, sendo
y=y(x) uma função dada implicitamente em cada caso por uma
equação:
a) 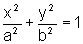 onde a e b são constantes não nulas.
onde a e b são constantes não nulas.
b) 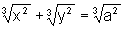 onde a é uma constante
onde a é uma constante
c) tg y=xy
d) arctg(x+y)=x
e) 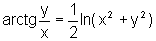
a) Sendo y(x)=arccos x, encontre y'.
b) Sendo y(x)=arccotg x, encontre y'.
c) Sendo y(x)=arcsec x, encontre y'.
d) Sendo y(x)=arccossec x, encontre y'.
![]() Sendo
Sendo 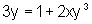 , encontre
a equação da reta tangente à curva definida por essa
equação, no ponto de abscissa 1.
, encontre
a equação da reta tangente à curva definida por essa
equação, no ponto de abscissa 1.
![]() Encontre a derivada de cada uma das funções dadas implicitamente
abaixo, no ponto indicado:
Encontre a derivada de cada uma das funções dadas implicitamente
abaixo, no ponto indicado:
a) 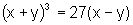 em (2,1)
em (2,1)
b) 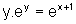 em (0,1)
em (0,1)
c) 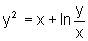 em (1,1)
em (1,1)
![]() Considerando
Considerando
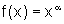 ,
, 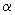 real, x>0, mostre que
real, x>0, mostre que 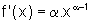 ,
fim de generalizar a Situação
3.
,
fim de generalizar a Situação
3.
![]() Sabendo que: sendo
f(x)=ex, a derivada é
Sabendo que: sendo
f(x)=ex, a derivada é 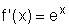 ,
mostre que se g(x)=ax, então
,
mostre que se g(x)=ax, então 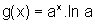 .
.
![]() Sabendo que: sendo
f(x)=ln x, a derivada é
Sabendo que: sendo
f(x)=ln x, a derivada é 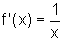 ,
mostre que se
,
mostre que se 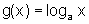 ,
então
,
então 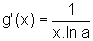 .
.
