A concavidade do gráfico de uma função num intervalo contido em seu domínio e os pontos de inflexão

Seja f uma função derivável num intervalo aberto I contido em seu domínio e x₀ um ponto de I.

A reta tangente ao gráfico de f no ponto (x₀,f(x₀)) é dada por:

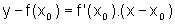
Ou seja, a reta tangente pode ser encarada como sendo o gráfico de uma função polinomial de primeiro grau T, dada por:

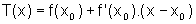
Definição: Dizemos que o gráfico de f tem concavidade para cima no intervalo aberto I quando f(x)>T(x) quaisquer que sejam x e x₀ em I, sendo .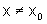

Analogamente, podemos definir o que vem a ser concavidade para baixo do gráfico de f.

Definição: Dizemos que o gráfico de f tem concavidade para baixo no intervalo aberto I quando f(x)<T(x) quaisquer que sejam x e x₀ em I, sendo .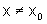

Finalmente, o ponto onde ocorre mudança de concavidade no gráfico tem um nome especial que é ponto de inflexão. Mais precisamente, temos:

Definição: Seja f uma função contínua e x₀ um ponto de seu domínio. O ponto x₀ é denominado um ponto de inflexão de f quando nele ocorre mudança de concavidade do gráfico de f.

Um resultado importante relaciona a derivada segunda da função com a concavidade do gráfico de f.

Propriedade: Seja f uma função derivável pelo menos até segunda ordem num intervalo aberto I.

a) Se f''(x)>0 em I, então o gráfico de f terá concavidade para cima em I.
b) Se f''(x)<0 em I, então o gráfico de f terá concavidade para baixo em I.