Nossa tarefa agora é calcular a derivada de algumas funções simples, utilizando a definição.

Seja f(x)=x³, cujo gráfico é o seguinte:

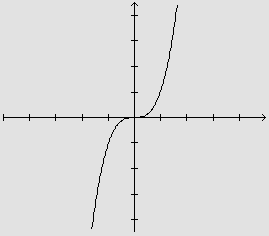
Para cada x real, temos definida uma nova função, denotada por f', denominada derivada da função f, que, em cada x fornece o valor do coeficiente angular da reta tangente ao gráfico de f. Nesse caso, temos
f'(x)=3x².

Seja agora 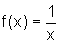. Graficamente, temos:

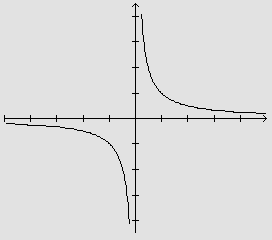
Observamos aqui que a função não está definida na origem. Assim, só tem sentido procurar a derivada quando x é diferente de zero. Tanto para x>0, como para x<0, encontramos que .

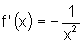Se 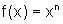, onde n é um número natural, então 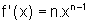, para todo x real.

Seja 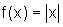, cujo gráfico é o seguinte:

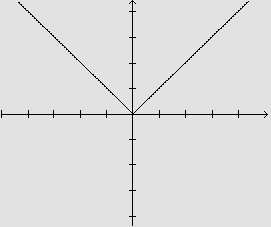
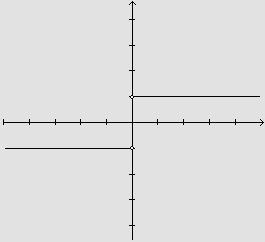
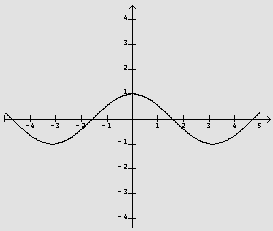
Geometricamente, percebemos que para os valores positivos de x, a reta tangente ao gráfico é uma reta com coeficiente angular 1; para os valores negativos de x, a reta tangente ao gráfico é uma reta com coeficiente angular -1. Para x=0 "parece" não existir reta tangente ao gráfico!

Isso significa que:

Seja .

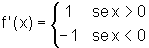
A função só está definida para os valores de x que são diferentes de zero.
Geometricamente, percebemos que para os valores positivos de x, a reta tangente ao gráfico é uma reta horizontal e que, portanto tem coeficiente angular igual a zero. O mesmo pode ser dito para os valores negativos de x.

Assim, a função 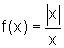é derivável em todos os pontos do seu domínio, sendo f'(x)=0, para todo x diferente de zero.

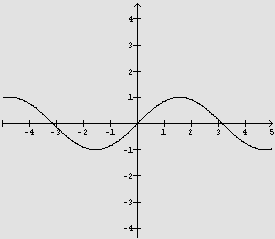
Seja f(x)=sen x, onde a variável x percorre o conjunto dos números reais, denotando a medida do arco em radianos ou o comprimento do arco em u.m.c.. A derivada de f, para todo valor de x, é f'(x)=cos x.

Seja f(x)=cos x, onde a variável x percorre o conjunto dos números reais, denotando a medida do arco em radianos ou o comprimento do arco em u.m.c.. A derivada de f, para todo valor de x, é f'(x)=-sen x.

Conclusão

Dada uma função, podemos assim, pela definição, investigar a existência de sua derivada em qualquer ponto do domínio, examinando determinado limite. Se a função for derivável em um ponto, existirá o limite examinado. Caso a derivada não exista em algum ponto, podemos chegar a essa conclusão, descobrindo que o determinado limite não existe. Entretanto, é evidentemente bastante trabalhoso agir dessa forma o tempo todo.
Existem alguns Teoremas, a respeito da existência e do cálculo de derivadas, que facilitam sobremaneira as investigações. São verdadeiros atalhos para o cálculo de derivadas.