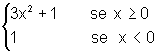Sendo , conclua que para x<0, também vale .

Determine a equação da reta tangente ao gráfico 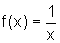de no ponto .

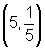Determine a equação da reta tangente ao gráfico de 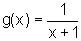que passa pelo ponto (-7,4). Compare com o Exercício 2 e encontre uma explicação razoável para o coeficiente angular dessa reta.

Dada a função f(x)=

a) Esboce o seu gráfico.
b) Verifique se f é derivável para x=0.
c) Mostre que, para x>0, f é derivável e encontre a derivada.
d) Mostre que, para x<0, f é derivável e encontre a derivada.
e) Escreva a expressão da derivada de f, dando o seu domínio, e esboce seu gráfico.

Dada a função f(x)=ln x, determine, pela definição, sua derivada onde ela existir. Dada a função inversa f ^-1(x)=e^x, determine sua derivada onde ela existir.

Deduza, a partir da derivada de f(x)=sen x, a derivada da função inversa:
f ^-1(x)=arcsen x.

Deduza, a partir da derivada de f(x)=cos x, a derivada da função inversa:
f ^-1(x)=arccos x.

Calcule a derivada de g(x)=arcsen(x+2).

Calcule a derivada de h(x)=3.e^x-4.
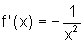