Movimento uniformemente variado

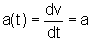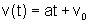Em Física, estudamos que esse movimento, apresenta variação uniforme da velocidade, isto é, sofre aceleração constante e, sendo , constante, podemos escrever , sendo v₀ a velocidade inicial, uma constante.

Com efeito, sendo 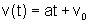, v é uma função cuja derivada é constante e igual a a.

Podemos então, estudar essa função utilizando argumentos matemáticos e inferindo interpretações físicas.

Observamos que a função 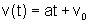, é uma função do primeiro grau em t, sendo assim, a constante v₀ é o coeficiente linear, ou seja, é a ordenada do ponto onde o gráfico, que é uma reta, encontra o eixo vertical, o que ocorre quando t=0. Por outro lado, a é o coeficiente angular da reta, ou seja, é a taxa de crescimento/decrescimento da função v.

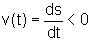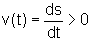Quando , s é uma função estritamente decrescente de t e quando , s é uma função estritamente crescente de t.

Como, por definição, 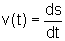, temos 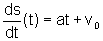, podemos escrever 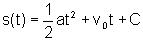, onde C=s(0), que é denominada a equação horária do movimento. O valor s(0), normalmente é denotado por s₀.

Dessa forma, a função que fornece o espaço percorrido, em se tratando de um movimento uniformemente variado é uma função do segundo grau em t, tendo, portanto, como gráfico, uma parábola.

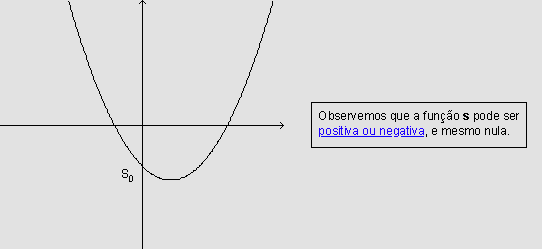
É preciso observar que as expressões "deslocamento de um móvel" e "espaço percorrido por um móvel" têm significados diferentes, não podendo ser confundidas. De fato, um corpo pode ir de A até B e depois voltar para A: dessa forma, o deslocamento total do móvel foi nulo, enquanto que o espaço percorrido é igual ao dobro da distância de A a B. Assim, o espaço percorrido é sempre uma distância sendo pois, um número não negativo.

Outras expressões que não podem ser confundidas são: "trajetória de um corpo em movimento" e "gráfico da função espaço percorrido". Com efeito, por exemplo, a equação horária pode ser dada por s(t)=2t²+3t+1, isto é, o gráfico da função espaço percorrido é uma parábola, enquanto que a trajetória pode ter sido numa linha reta.

Uma observação ainda é necessária: qual significado físico do fato da variável t, tempo, poder assumir valores positivos ou negativos ou mesmo zero?

Em t=0, o fenômeno, isto é, o movimento do objeto, começou a ser observado.

Quando t>0, naturalmente, o tempo está passando e está ocorrendo a observação do fenômeno.

Quando t<0, em Física, nada podemos afirmar sobre o fenômeno. Em termos matemáticos, podemos interpretar que, antes do cronômetro ser acionado, o corpo obedecia à equação horária s(t)=2t²+3t+1.

No contexto da Física, em geral, 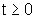, pois o estudo do movimento será convenientemente realizado a partir de t=0.

Exemplo: Vamos analisar o movimento de um corpo, cuja equação horária é dada pela equação: .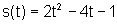

Temos: 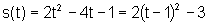cujo gráfico é o seguinte:

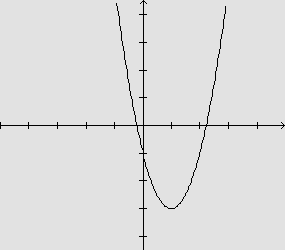
Vejamos:

• quando t<0, não estava ocorrendo a observação do fenômeno, logo tal fato não é relevante para um físico.
•quando 0<t<1, a velocidade uniformemente variável é negativa - observe o coeficiente angular da reta tangente ao gráfico - o movimento é retardado. A função s é decrescente até atingir s=-3.
• quando t=1, a velocidade é zero - observe o coeficiente angular da reta tangente ao gráfico.
• quando t>1, a velocidade uniformemente variável é positiva - observe o coeficiente angular da reta tangente ao gráfico - o movimento é acelerado. A função s é crescente.

No trecho em que s<0, o movimento está acontecendo em sentido contrário ao que foi adotado no referencial estabelecido.