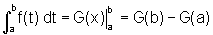A fim de demonstrar o Teorema Fundamental do Cálculo vamos inicialmente apresentar uma outra propriedade que será utilizada em sua demonstração.

Teorema da Média: Seja f uma função contínua num intervalo [a,b]. Então existe um ponto x₀ nesse intervalo tal que:

.

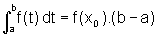Demonstração:

A partir da definição de integral definida de f em [a,b], temos:

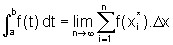
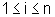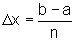onde x_i*, para , é um ponto qualquer do i-ésimo sub-intervalo de comprimento em que o intervalo [a,b] foi dividido.

Como f é contínua em [a,b], pelo Teorema de Weierstrass, existem m e M no intervalo tais que para qualquer ,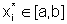

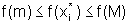
ou seja, m e M são, respectivamente os pontos de mínimo e de máximo da função f em [a,b].

Podemos então dizer que:

,

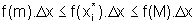e, somando para i variando de 1 a n, temos

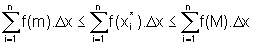
de onde,

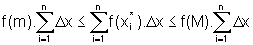
isto é,

.

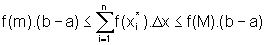Calculando o limite quando 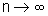, temos:

ou seja,

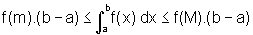
de onde

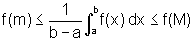
Logo, 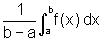está compreendido entre o valor mínimo e o valor máximo da função f em [a,b]. Como f é contínua, por hipótese, existe um ponto x₀ nesse intervalo tal que 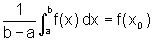, como queríamos mostrar.

Teorema Fundamental do Cálculo: Seja f uma função contínua no intervalo [a,b]. A função F, dada por 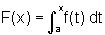, é derivável em todos os pontos interiores ao intervalo ]a,b[ e sua derivada é dada por F'(x)=f(x).

Demonstração:

Precisamos mostrar que F é derivável em ]a,b[, ou seja que existe

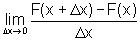, para todo x em ]a,b[.

Mais ainda, precisamos mostrar que esse limite é igual a f(x).

Para cada x em ]a,b[, temos:

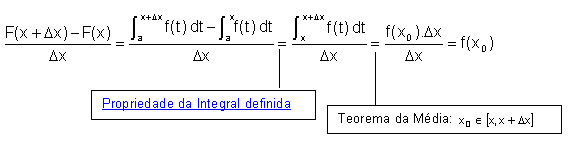
Quando 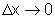, como f é contínua, temos 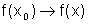, ou seja existe o limite do quocient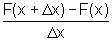e e

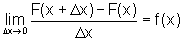
ou seja,

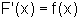
como queríamos mostrar.

Conseqüência: Se f é uma função contínua no intervalo [a,b], então 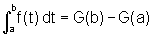, onde G é uma qualquer primitiva de f, isto é, tal que G'=f.

Demonstração:

O Teorema Fundamental do Cálculo garante que se 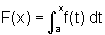então a função F é uma primitiva de f, pois 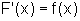, precisamente aquela que se anula para x=a, uma vez que .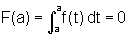

Seja G uma outra primitiva qualquer de f, isto é

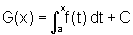
Temos então,

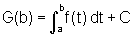
e

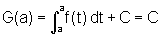
Logo, 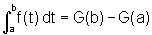, como queríamos mostrar.

 

Notação: