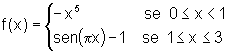![]() Calcular as áreas das regiões delimitadas pelas curvas:
Calcular as áreas das regiões delimitadas pelas curvas:
a) 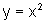 e
e 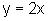
b) 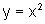 +3
e
+3
e 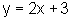
c) 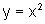 -3
e
-3
e 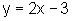
É possível estabelecer alguma conclusão a partir das áreas calculadas?
![]() Calcular as áreas das regiões limitadas e que são
delimitadas por:
Calcular as áreas das regiões limitadas e que são
delimitadas por:
a) eixo x e 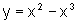
b) eixo y e 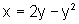
c) 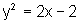 e
e 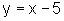
![]() Encontrar uma primitiva F da função
Encontrar uma primitiva F da função 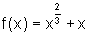 que satisfaça F(1)=1.
que satisfaça F(1)=1.
![]() Encontrar uma função f tal que
Encontrar uma função f tal que 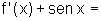 0 e f(0)=2.
0 e f(0)=2.
![]() Uma partícula desloca-se sobre um eixo horizontal com velocidade
Uma partícula desloca-se sobre um eixo horizontal com velocidade
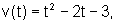 com
com 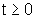 .
Determinar o espaço percorrido entre os instantes t=0 e t=4,
bem como o deslocamento da partícula.
.
Determinar o espaço percorrido entre os instantes t=0 e t=4,
bem como o deslocamento da partícula.
Observação:
Definimos o deslocamento do objeto, entre os instantes t=a e
t=b, como sendo 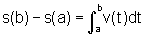 ,
enquanto que o espaço percorrido pelo objeto entre os
instantes t=a e t=b é obtido através da
,
enquanto que o espaço percorrido pelo objeto entre os
instantes t=a e t=b é obtido através da 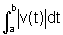 .
.
![]() Desenhar, em cada caso, o conjunto envolvido e determinar sua área:
Desenhar, em cada caso, o conjunto envolvido e determinar sua área:
a) B é o
conjunto limitado pelos gráficos de 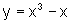 e
e 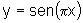 , com
, com
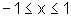
b) B é o
conjunto de todos os pontos (x,y) tais que 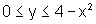
c) B é o
conjunto limitado pelas retas x=0 e 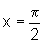 ;
e pelos gráficos
;
e pelos gráficos 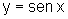 e
e 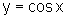 .
.
d) 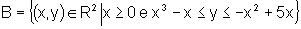
![]() Usando o Teorema Fundamental do Cálculo, obter a derivada de
cada uma das funções seguintes:
Usando o Teorema Fundamental do Cálculo, obter a derivada de
cada uma das funções seguintes:
a) 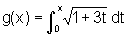
b) 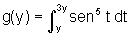
c) 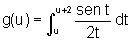
d) 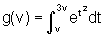
e) 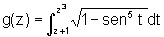
![]() Encontrar o valor das integrais definidas:
Encontrar o valor das integrais definidas:
a) 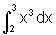
b) 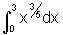
c) 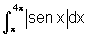
d) 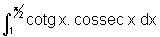
e) 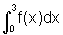 ,
sendo
,
sendo