Em primeiro lugar,
•
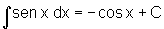que é
imediata.
•
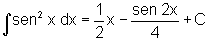, resultado
que encontramos quando a resolvemos através de transformações
trigonométricas ou por
partes.
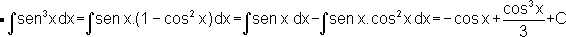
O fato de termos um expoente ímpar nos permite separar
um dos fatores e escrever os outros em função do cosseno,
a fim de resolvermos a integral por substituição.
• 
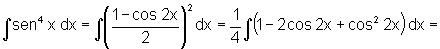
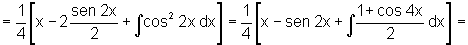
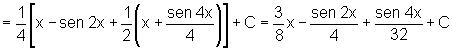
O fato do expoente ser par, não nos permite o raciocínio anterior. Entretanto, através da transformação trigonométrica, conseguimos "abaixar" o grau.
As integrais análogas envolvendo a função cosseno são resolvidas da mesma maneira.
Continuando a exploração, temos:
•
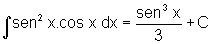que resolvemos
por substituição.
•
que resolvemos
por substituição.
• 
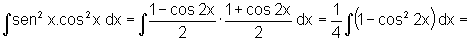
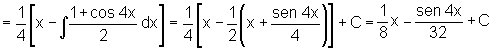
Observamos nessa integral o múltiplo uso das transformações trigonométricas.
Poderíamos
continuar o mesmo tipo de raciocínio. No Exercício
3 temos mais dois exemplos onde os expoentes são maiores.
 |
 |