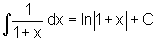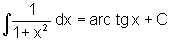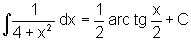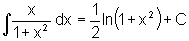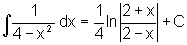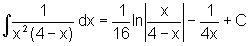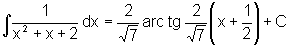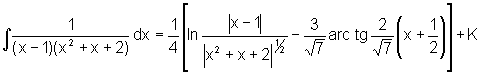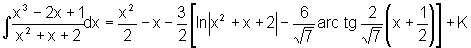Primitivação por frações parciais
Esta técnica é utilizada quando precisamos encontrar a família de primitivas de uma função que é dada por uma fração racional, isto é, pelo quociente de dois polinômios. Os primeiros exemplos são muito simples e, na verdade, não apresentam nada de novo.
O primeiro exemplo envolve uma substituição bem fácil:
O segundo é
um exemplo importante, mas também é fácil
pois é uma primitiva
imediata.
Um exemplo um pouco
mais geral pode ser o seguinte:
No exemplo a seguir,
a função integrando é uma fração
racional e resolvemos a integral através de uma substituição,
já que, no numerador temos "quase" a derivada da função
que aparece no denominador.
No exemplo seguinte
precisamos da nova técnica:
De modo geral, uma função racional pode ser decomposta
numa soma de frações mais simples e, por isso, dizemos
que fazemos a decomposição em frações parciais.
Evidentemente, se o grau do polinômio do numerador for maior ou
igual ao grau do polinômio do denominador, em primeiro lugar,
efetuamos a divisão dos polinômios, para separar a "parte
inteira". Depois decompormos a fração resultante
em frações parciais.
A decomposição é feita com base em quatro Teoremas de Existência que, basicamente, resolvem o problema:
 Sejam
a, b, a, b, números
reais, com
Sejam
a, b, a, b, números
reais, com 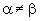 .
Então, existem números reais A e B, tais que:
.
Então, existem números reais A e B, tais que:
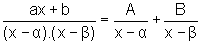
 Sejam a, b, números
reais, com
Sejam a, b, números
reais, com 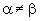 e P um polinômio cujo grau é estritamente menor que 3.
Então, existem números reais A, B e D, tais que:
e P um polinômio cujo grau é estritamente menor que 3.
Então, existem números reais A, B e D, tais que:
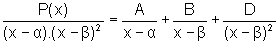
![]() Sejam b, c, a, números reais e P um
polinômio cujo grau é estritamente menor que 3. Suponhamos
ainda que
Sejam b, c, a, números reais e P um
polinômio cujo grau é estritamente menor que 3. Suponhamos
ainda que 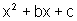 não admite raízes reais, isto é, seu discriminante
é menor que zero. Então, existem números reais
A, B e D, tais que:
não admite raízes reais, isto é, seu discriminante
é menor que zero. Então, existem números reais
A, B e D, tais que:
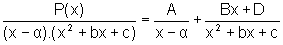
 Sejam b, c, a , números reais e P
um polinômio cujo grau é estritamente menor que 5. Suponhamos
ainda que
Sejam b, c, a , números reais e P
um polinômio cujo grau é estritamente menor que 5. Suponhamos
ainda que 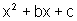 não admite raízes reais, isto é, seu discriminante
é menor que zero. Então, existem números reais
A, B, D, E e F, tais que:
não admite raízes reais, isto é, seu discriminante
é menor que zero. Então, existem números reais
A, B, D, E e F, tais que:
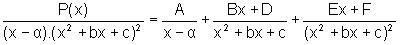
Precisamos observar que o polinômio do denominador sempre pode
ser decomposto num produto de fatores de primeiro e segundo graus.
Os fatores de primeiro grau aparecem quando existem raízes reais;
as raízes complexas são responsáveis pelos fatores
de segundo grau.
Evidentemente, todos esses teoremas poderiam ser enunciados numa forma mais geral. O que precisa estar claro é que o grau do polinômio do numerador deve ser estritamente menor do que o grau do polinômio do denominador, para podermos efetuar a decomposição em frações parciais. Se esse não for o caso, primeiro fazemos a divisão de polinômios, a fim de tornar o problema mais simples, como no Exemplo 9.