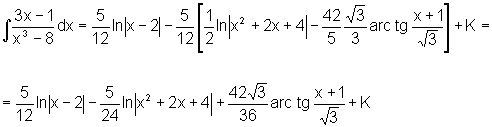Para calcular 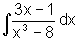, observamos, em primeiro lugar, que o denominador pode ser fatorado:

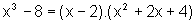
Como o termo de segundo grau tem discriminante negativo, usamos o Teorema 3 para fazer a decomposição em frações parciais:

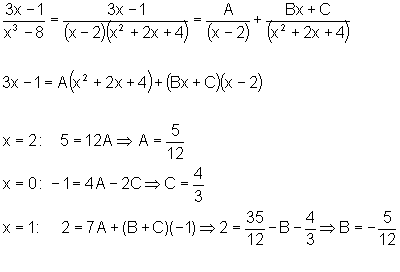
Logo,

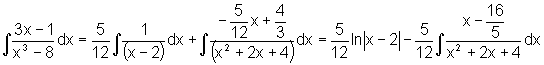
Seja

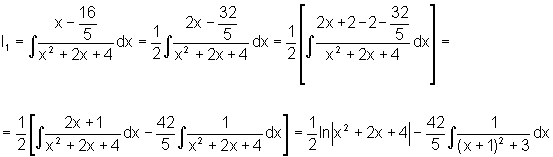
Na última integral podemos usar o mesmo raciocínio efetuado no Exemplo 7.

E assim,

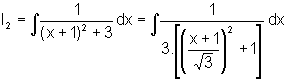
Fazemos:

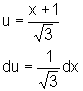
e, portanto,

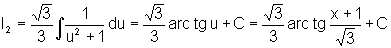
Finalmente, a solução da integral proposta inicialmente é: