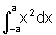 ,
,
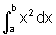 e
e 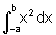 ,
onde a e b são números estritamente positivos,
com a<b.
,
onde a e b são números estritamente positivos,
com a<b. ![]() Calcule a área da região limitada pelas curvas
Calcule a área da região limitada pelas curvas 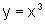 ,
x=0, x=a>0 e y=0. Obtenha uma fórmula geral para
,
x=0, x=a>0 e y=0. Obtenha uma fórmula geral para 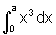 .
.
![]() Calcule as integrais
Calcule as integrais 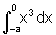 ,
,
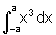 ,
, ![]() e
e 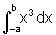 , para
a e b estritamente positivos, com a<b.
, para
a e b estritamente positivos, com a<b.
![]() Encontre a área da região limitada pelas curvas:
Encontre a área da região limitada pelas curvas:
a) y=x3,
x=-a, x=0 e y=0, sendo a>0.
b) y=x3, x=-a, x=a e y=0, sendo
a>0.
c) y=x3, x=-a, x=b e y=0, sendo
0<a<b.
As respostas coincidem
com 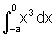 ,
, 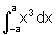 e
e 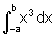 ? Justifique
sua resposta.
? Justifique
sua resposta.
![]() Seja
Seja 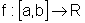 contínua
e
contínua
e 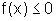 , para
todo x pertencente ao intervalo [a,b]. Descreva a área da região
delimitada por y=f(x) , x=a, x=b e y=0 em termos da integral de f no
intervalo [a,b].
, para
todo x pertencente ao intervalo [a,b]. Descreva a área da região
delimitada por y=f(x) , x=a, x=b e y=0 em termos da integral de f no
intervalo [a,b].
![]() Descreva, em termos de integrais, a área da região delimitada
por y=f(x), y=g(x), x=a e x=b, supondo que
Descreva, em termos de integrais, a área da região delimitada
por y=f(x), y=g(x), x=a e x=b, supondo que 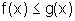 ,
,
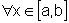 .
.
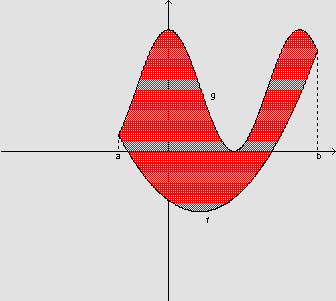
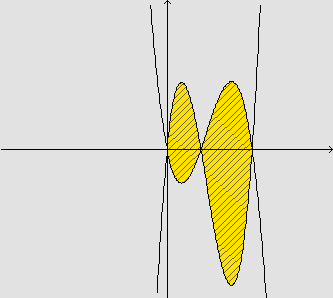
![]() Descreva em termos de integrais a área da região indicada
na figura:
Descreva em termos de integrais a área da região indicada
na figura:
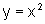 ,
,
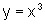 ,
, 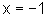 ,
,
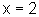 .
.