Corolário: Se duas funções contínuas têm derivadas iguais nos pontos interiores a I, então elas diferem por uma constante.
Prova:
Basta considerar
a função 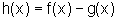 ,
onde f e g são as funções que têm
derivadas iguais no interior de um intervalo I.
,
onde f e g são as funções que têm
derivadas iguais no interior de um intervalo I.
Então 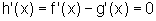 ,
pela hipótese.
,
pela hipótese.
Logo, pela Propriedade
anterior, 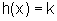 e, portanto,
e, portanto, 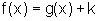 ,
para todo
,
para todo 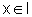 ,
como queríamos provar.
,
como queríamos provar.
