Sendo g a função dada por seu gráfico e considerando G qualquer uma das primitivas de g, isto é, G'(x)=g(x), para todo x,

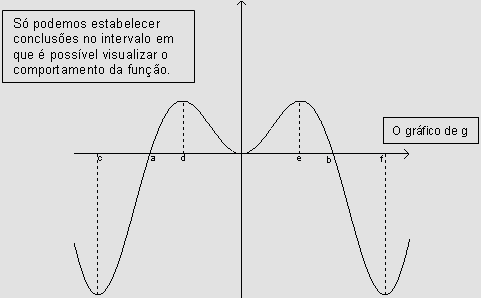
sabemos que, a partir do sinal da função primeira derivada de G, que é g=G', obtemos informações a respeito do comportamento de G, quanto ao seu crescimento ou decrescimento. Assim,

• quando x<a, g(x)<0, ou seja, G'(x)<0 e, portanto, G é estritamente decrescente;
• quando a<x<0, g(x)>0, ou seja, G'(x)>0 e, portanto, G é estritamente crescente;
• quando 0<x<b, g(x)>0, ou seja, G'(x)>0 e, portanto, G é estritamente crescente;
• quando x>b, g(x)<0, ou seja, G'(x)<0 e, portanto, G é estritamente decrescente.

Logo, x=a é um ponto de mínimo local para G, enquanto que x=b é um ponto de máximo local para G.

Por outro lado, a partir do gráfico de g=G', podemos esboçar o gráfico de g'=G'', pois percebemos o sinal do coeficiente angular da reta tangente, avaliando onde ele é negativo, nulo ou positivo. E a partir do gráfico de g'=G'' podemos obter informações a respeito da concavidade do gráfico de G.

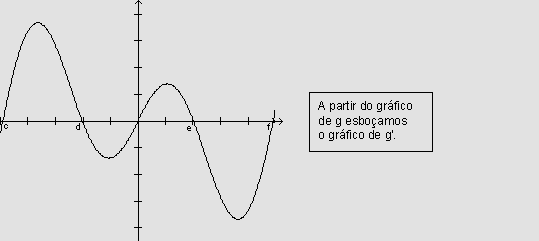
Assim, no gráfico de g', observamos que

• quando x<c, g'(x)<0, ou seja, G"(x)<0 e, portanto, o gráfico de G é côncavo para baixo;
• quando c<x<d, g'(x)>0, ou seja, G''(x)>0 e, portanto, o gráfico de G é côncavo para cima;
• quando d<x<0, g'(x)<0, ou seja, G''(x)<0 e, portanto, o gráfico de G é côncavo para baixo;
• quando 0<x<e, g'(x)>0, ou seja, G''(x)>0 e, portanto, o gráfico de G é côncavo para cima;
• quando e<x<f, g'(x)<0, ou seja, G''(x)<0 e, portanto, o gráfico de G é côncavo para baixo;
• quando x>f, g'(x)>0, ou seja, G''(x)>0 e, portanto, o gráfico de G é côncavo para cima.

E, portanto, x=c, x=d, x=0, x=e e x=f são pontos de inflexão para a função G, pois nesses pontos ocorre mudança de concavidade no gráfico.

Em nosso caso, estamos procurando a particular primitiva G tal que G(0)=1. No gráfico observamos qual é essa curva.