Para calcular 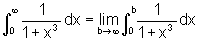, em primeiro lugar calculamos:

.

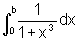Para tanto, vamos utilizar a técnica de primitivação por frações parciais, uma vez que

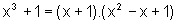
sendo que o fator do segundo grau é irredutível, isto é tem discriminante .

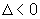Assim, pelo Teorema 3,

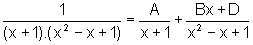
de onde obtemos:

,

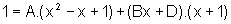onde temos dois polinômios idênticos, ou seja, a igualdade entre eles vale para qualquer valor real da variável x. Em particular, quando

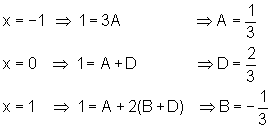
Daí podemos escrever:

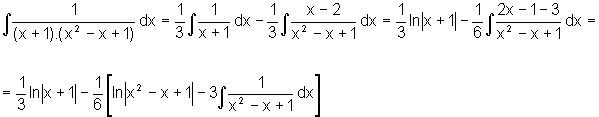
Na última integral I₁, o polinômio do denominador tem discriminante negativo, logo, completando os quadrados, temos:

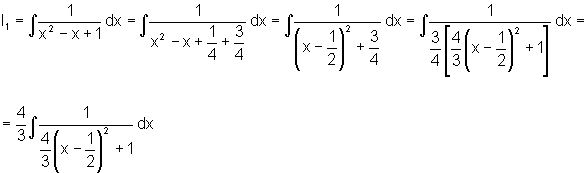
Fazendo

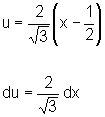
temos:

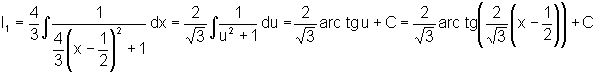
Assim,

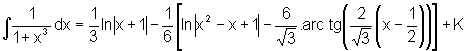
e, portanto,

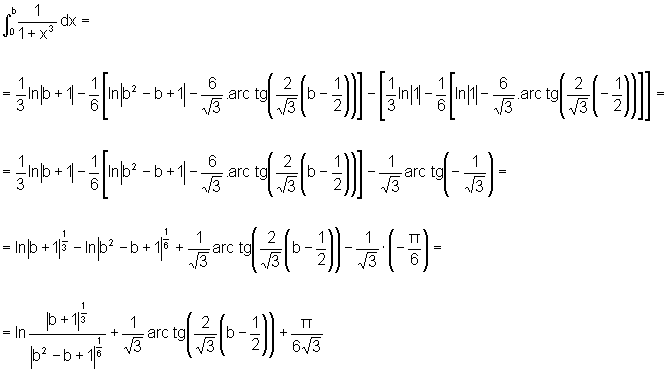
Finalmente,

.

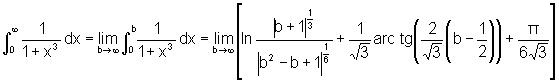Como

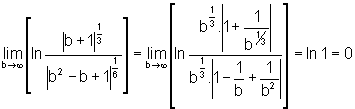
e

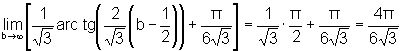
temos

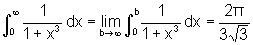
e, portanto, a integral dada converge.