![]()
Nosso objetivo é achar uma expressão para o cálculo da área da região compreendida entre o eixo x e a curva y=x2 para x variando no intervalo [0,k], onde k é um valor real qualquer.
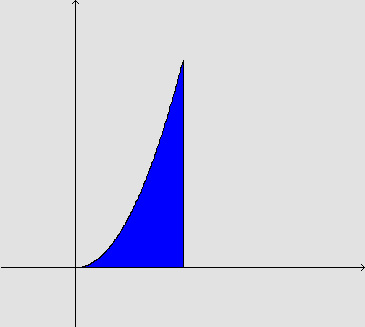
Vamos calcular essa área por falta e por excesso.
• Cálculo da área da região compreendida entre o eixo x e a curva y= x2 para x variando no intervalo [0,k], onde k é um valor real qualquer, aproximada por falta:
Dividimos o intervalo [0,k] em n partes iguais.

Dessa forma, cada sub-intervalo tem comprimento igual a  .
.
O i-ésimo
sub-intervalo, para 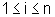 ,
determina um retângulo cuja base mede
,
determina um retângulo cuja base mede  e cuja altura
é
e cuja altura
é 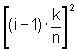 .
.

Dessa forma, a área aproximada por falta é dada por:
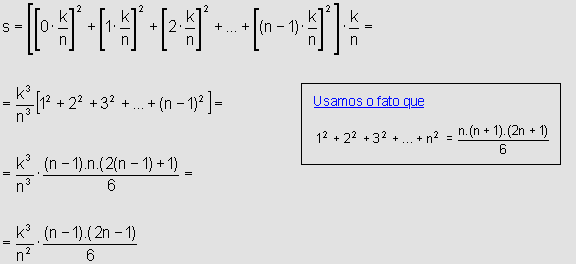
• Cálculo da área da região compreendida entre o eixo x e a curva y=x2 para x variando no intervalo [0,k], onde k é um valor real qualquer, aproximada por excesso:
Dividimos o intervalo [0,k] em n partes iguais.

Dessa forma, cada sub-intervalo tem comprimento igual a 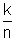 .
.
O i-ésimo sub-intervalo, para 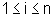 ,
determina um retângulo cuja base mede
,
determina um retângulo cuja base mede 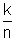 e cuja altura
é
e cuja altura
é 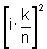 .
.
Dessa forma, a área aproximada por excesso é dada
por:
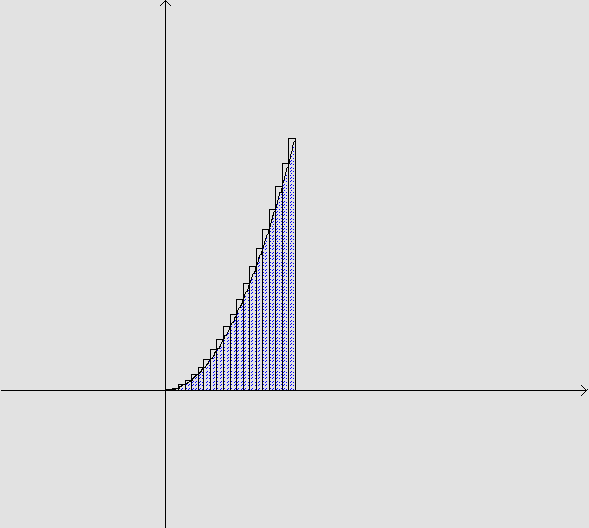

Assim, a área da região, dependendo do número n
de divisões do intervalo [0,k], está compreendida entre
dois valores:

Fazendo o número n de divisões do intervalo [0,k],
crescer indefinidamente, temos:
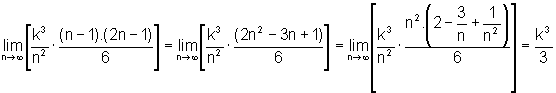
e
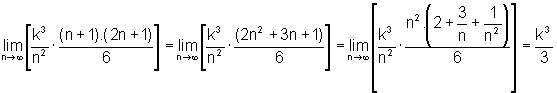
Logo, pelo Teorema do Confronto,
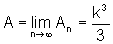 .
.
Isso significa que,
por exemplo, a área da região compreendida entre o eixo
x e a curva  para x variando no intervalo [0,4], é
para x variando no intervalo [0,4], é 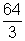 unidades de medida de área.
unidades de medida de área.
