A área da região que se encontra entre a parábola y = x² e o eixo x, para x variando no intervalo [-2,2].

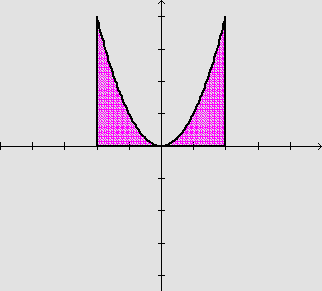
Para calcular a área da região descrita acima, não temos nesse momento resultado algum que nos permita fazê-lo rápida e exatamente.

Observemos, em primeiro lugar, que por uma questão de simetria, basta se calcular a área de metade da região; em seguida, multiplicar por 2 o resultado encontrado. Em segundo lugar, no caso presente, temos condição de fazer um cálculo aproximado para a área da região. Vejamos:

• Dividindo o intervalo [0,2] em quatro partes iguais, podemos encontrar 4 retângulos construídos de modo que a base superior esteja sempre por baixo da curva. A soma das áreas desses retângulos fornece um valor aproximado por falta para a área:

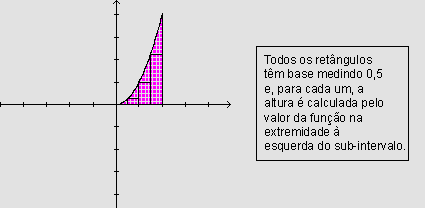
• Dividindo o intervalo [0,2] em quatro partes iguais, podemos encontrar 4 retângulos construídos de modo que a base superior esteja sempre por cima da curva. A soma das áreas desses retângulos fornece um valor aproximado por excesso para a área:

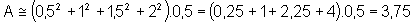
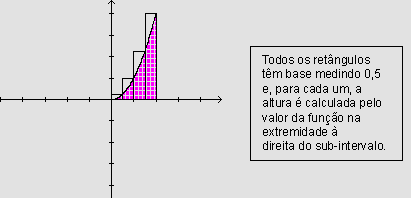
Assim, a área da região que se encontra entre a parábola y = x² e o eixo x, para x variando no intervalo [-2,2] está entre 2.(1,75)=3,5 e 2.(3,75)=7,5, ou seja:

• Dividindo o intervalo [0,2] em oito partes iguais, podemos encontrar 8 retângulos construídos de modo que a base superior esteja sempre por baixo da curva. A soma das áreas desses retângulos fornece um valor aproximado por falta para a área:

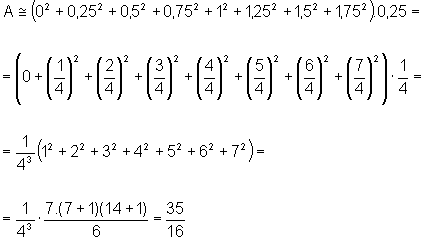
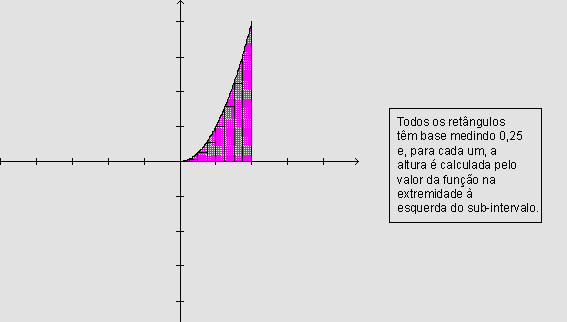
• Dividindo o intervalo [0,2] em oito partes iguais, podemos encontrar 8 retângulos construídos de modo que a base superior esteja sempre por cima da curva. A soma das áreas desses retângulos fornece um valor aproximado por excesso para a área:

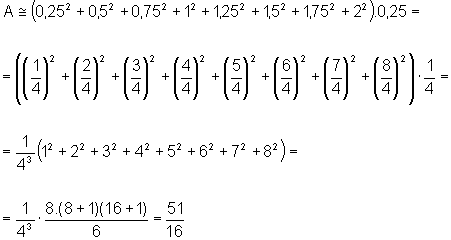
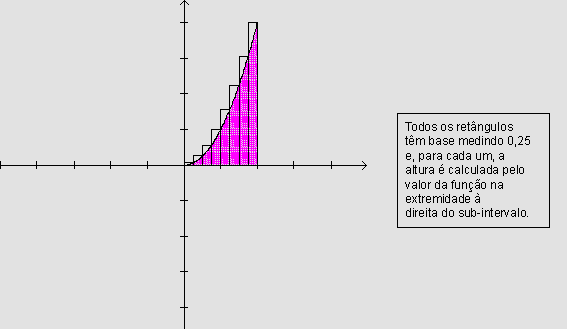
Assim, a área A da região que se encontra entre a parábola y = x² e o eixo x, para x variando no intervalo [-2,2] é tal que 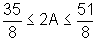, ou seja:

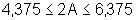
Podemos notar que, aumentando o número de sub-intervalos, melhor é a aproximação do valor da área da região considerada.