Como o círculo é simétrico em relação aos eixos x e y, basta calcular a área de um quarto dele e fazer a multiplicação do resultado por 4.

A circunferência do círculo, facilitando os cálculos, pode ser considerada com centro na origem e raio unitário. Assim, tomando o intervalo [0,1], podemos considerar a função 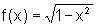, cujo gráfico fornece o arco situado no primeiro quadrante.

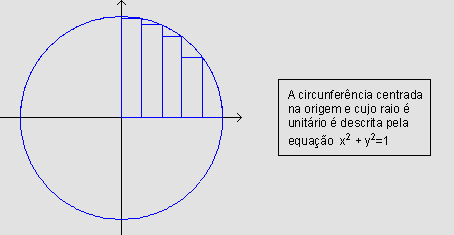
Então, dividindo o intervalo [0,1] em 5 sub-intervalos iguais e calculando a área de cada um dos retângulos obtidos, temos o seguinte resultado:

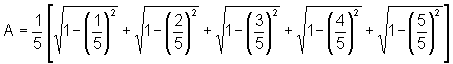
pois todos os pequenos retângulos têm base 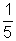e a altura, em cada um, é dada pelo valor da ordenada da funçã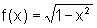o , calculada na extremidade à direita de cada sub-intervalo.

Assim:

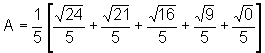
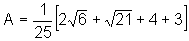
ou seja,

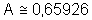
Dessa maneira,

Esse valor é, em certo sentido, esperado, pois uma parte do círculo não entrou no cálculo da área. Como calculamos a área aproximada por falta, o valor obtido é menor do que o valor real da área do círculo que, por ter raio unitário, sabemos ser p. Entretanto, evidentemente, se utilizássemos um número maior de sub-intervalos, obteríamos um valor mais próximo de p.