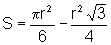Dado um arco de circunferência, cujo comprimento é l, ligando suas extremidades ao centro da circunferência, determinamos uma região do plano, denominada setor circular.

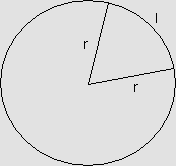
A fim de encontrar a área do setor circular, podemos estabelecer a seguinte proporção:

de onde, temos:

Observamos que, em nosso problema, a área do setor circular pode ainda ser considerada como a soma das áreas: de um triângulo e aquela S da região compreendida entre o arco e a corda da circunferência determinada pelas extremidades do arco.

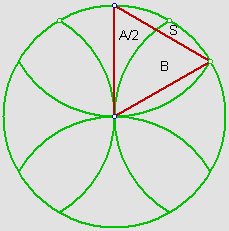
Nesse caso, a circunferência foi dividida em 6 setores iguais, cada um deles, conseqüentemente, com área 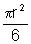. Assim, a área S da região é dada por: